The Revisions to Gross Domestic Product, Gross Domestic Income, and Their Major Components
Now more than ever, the private sector and policymakers rely on the National Income and Product Accounts (NIPAs) to provide a timely, comprehensive, and accurate picture of the condition of the U.S. economy to inform economic decisions.
The two featured measures in this study, gross domestic product (GDP) and gross domestic income (GDI), are the two most used measures to assess a country's economic pulse, and that is why, throughout this study, we systematically analyze GDP and GDI data releases in search of possible ways to improve the methods by which we aggregate and report data at different frequencies and in different sectors of the economy.
GDP measures activity as the sum of all final expenditures in the economy; it is detailed on the product side of the domestic income and product account. Meanwhile, GDI measures activity as the sum of all incomes generated in production; it is detailed on the income side of the account. By design, the flows of final expenditures and incomes generated are equal, but in practice, they differ because each is estimated from largely different source data. The difference between GDP and GDI is allocated to the income side of the domestic income and product account and is known as the statistical discrepancy.
Measuring the accuracy of national account estimates is challenging because it is impossible to know the true values of the estimates. This measurement challenge is long-standing and derives from three principal facts about the compilation of the estimates. First, the earliest GDP and GDI estimates are based on partial and preliminary data and on trend projections when data are not available. Second, the source data for the early estimates in the NIPAs come from a mixture of survey, tax, and other business and administrative data as well as various indicators, such as heating degree days; these data are subject to a mix of sampling and nonsampling errors and biases that cannot be assessed. Third, the NIPAs are regularly revised to reflect changes in the economic concepts and methods necessary for the accounts to provide an accurate picture of the evolving U.S. economy.1 For example, in the 2013 comprehensive revision of the NIPAs, a new category of investment—intellectual property products (IPP)—was formed; it consists of research and development; entertainment, literary, and artistic originals; and software. This last component, software, was also measured before, but was bundled with equipment in a category called equipment and software. In addition, seasonal adjustment factors were updated to reflect changing seasonal patterns. Given the measurement challenges, accuracy cannot be assessed by conventional statistical measures, such as standard errors. Instead, the Bureau of Economic Analysis (BEA) focuses on the reliability of the estimates, which can be assessed by examining the sizes and patterns of revisions to estimates (see the box “Accuracy, Reliability, and Uncertainty”).
Because the revisions are repeated estimations of the economic activity in a period, their pattern and magnitude provide a measure of the reliability of the estimates. Some revisions are due to the replacements of early extrapolations for missing source data, preliminary survey data, or the replacement of indirect indicators with revised and more complete data, such as annual data and census data. However, some of the revisions are the result of updates to the concepts on which the accounts are based, as with the 2013 comprehensive revision mentioned above.
BEA's principal standard of reliability is based on the revisions from its early estimates to its “latest” estimates, most of which have been through at least one comprehensive revision (see the box “Vintages and Timing of Revisions” for the detailed revision schedule ).
Because the latest vintage incorporates the most recent comprehensive revision, it incorporates all the available source data that are believed to be the most reliable.
More specifically, BEA judges the qualitative reliability of its early estimates by whether they present the same general picture of economic activity as the latest estimates in terms of the following: 1) long-term growth rates; 2) trends in saving, investment, government spending, corporate profits, and other key components of GDP and GDI; 3) broad features of the business cycle, including the timing and depth of recessions, the strength of recoveries, and the major components contributing to growth and contractions; and 4) the patterns of quarterly growth, including whether growth in any period is high or low relative to the trend, is accelerating or decelerating, or is positive or negative.
As we will show in the following sections, both the pattern and the magnitude of the revisions indicate that the early estimates are reliable. That is, the revisions do not substantively change BEA's measures of long-term growth, the picture of business cycles, and the trends in major components of GDP and GDI. In short, the early estimates provide a consistent and reliable picture of general economic activity. Given the general accuracy of the early estimates, policymakers should be able to rely on these estimates as accurate measures of economic activity.
Quantitatively, revisions are measured as the changes from an earlier vintage of a given estimate to a later vintage of that estimate, for example, from the advance estimate to the latest estimate. There are three early vintages of “current quarterly” estimates of GDP—the advance estimates (released a month after the quarter ends), the second estimates (released 2 months after the quarter ends), and the third estimates (released 3 months after the quarter ends). Each estimate is produced using a wide mix of source data—preliminary survey results, such as the Census Bureau's Survey of Retail Sales and Services, and manufacturers' shipments, various indicators, trade industry data and more—that are later revised to reflect more complete information or to replace trend projections.
BEA examines qualitative measures of reliability that focus on the overall performance of the three vintages of the current quarterly estimates of growth, relative to the latest quarterly estimates of growth. More specifically, the qualitative measures address two questions about current-dollar GDP and current-dollar GDI.
- Does the sign (+/−) of all the current quarterly vintages of estimates of growth match that of the latest estimate? This is a measure of directional reliability. For GDP, the signs match 95 percent of the time, and for GDI, 92 percent of the time.
- Do the magnitudes of all the current quarterly estimates fall above, within, or below one standard deviation of the mean growth of the latest estimate over the period? This is a measure of reliability relative to trend. For 1996–2018, the latest estimates of GDP had a mean of 4.42 percent and a standard deviation of 2.72, and the current quarterly vintages fell within one standard deviation of the mean (between1.71 and 7.15) about 78 percent of the time. For GDI, the corresponding mean is 4.50 percent and the standard deviation is 3.11, and the current quarterly vintage fell between one standard deviation of the mean (between 1.38 and 7.61), also about 78 percent of the time.
It is important to note that the frequency counts were based on a comparison between all the current quarterly vintages available for a quarter and the latest quarterly vintage for that quarter. For GDP, there are always three current quarter estimates to compare, the advance, second, and third, but for GDI, from 1996 to the end of 2003, the available current quarter estimates are only second (expect for fourth quarters) and third, and from 2004 on, the fourth estimate is also available, and therefore included in our comparisons with the latest estimate.
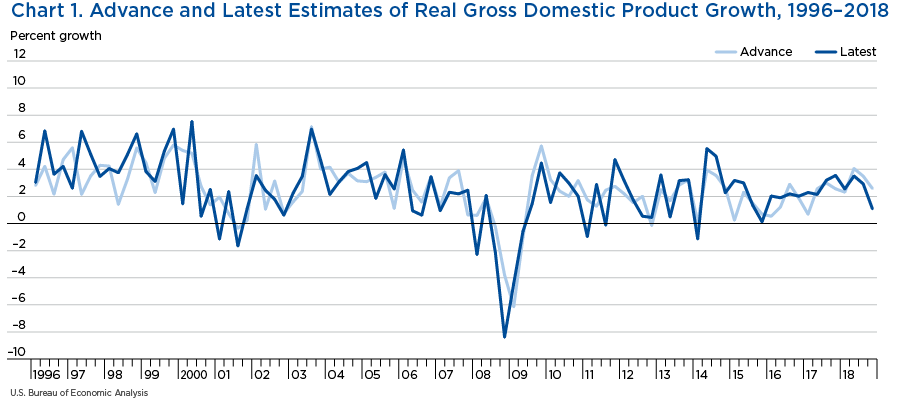
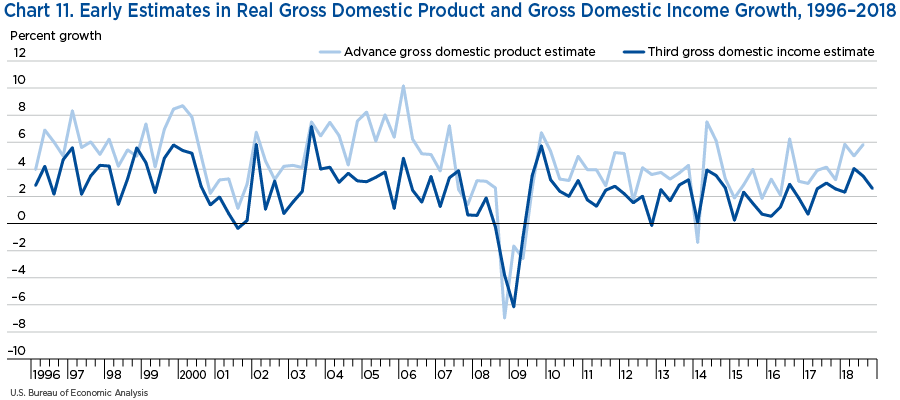
As a preview of the analysis, chart 1 provides an illustration of this point by plotting advance estimates of real GDP growth over 22 years, from 1996 to 2018, against the latest estimates.2
Chart 1 shows that, with few exceptions such as the Great Recession period and a couple more quarters throughout the sample, the overall pattern of movement in GDP is little changed by revisions. The Uncertainty Around Turning Points section will provide a more detailed analysis of the estimates' revisions around the two recessions included in the sample.
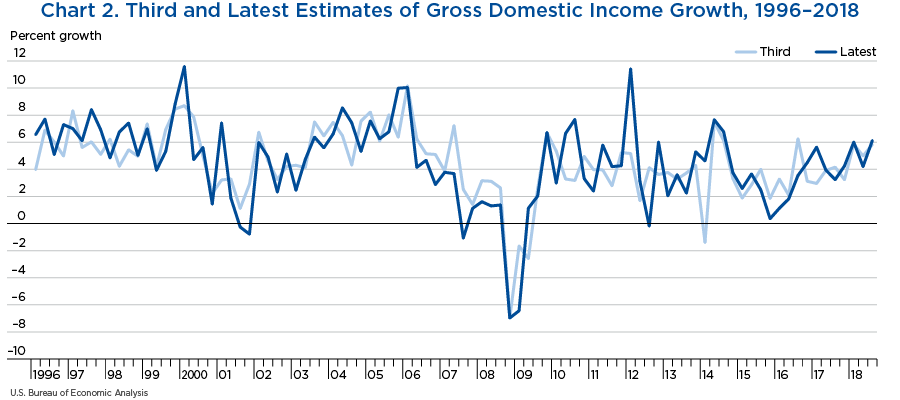
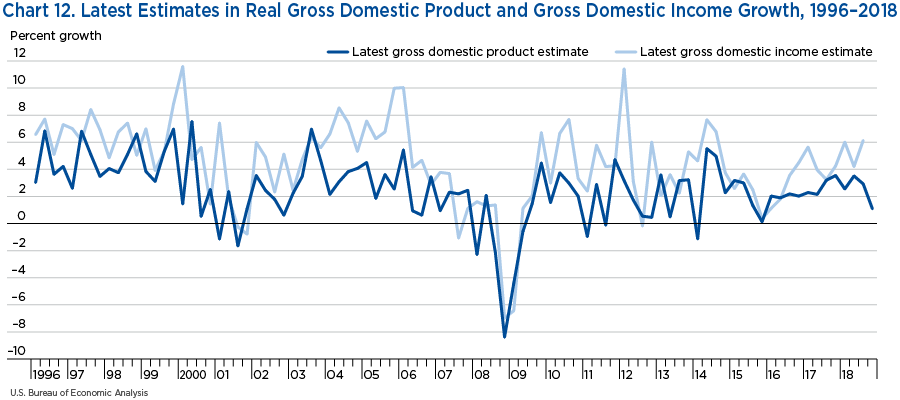
A similar picture emerges for the third estimate of GDI versus the latest estimates (chart 2).
The remainder of this article is organized as follows:
- A discussion of revisions to quarterly estimates of GDP and its components;
- A closer look at the new category introduced in the 2013 comprehensive revision called intellectual property products and its comparison to other closely related investment categories;
- A section covering the revisions to quarterly estimates of GDI and its components;
- An evaluation of growth revisions during and around recessions' turning points, both at the beginning and at the end of recessions, to try to evaluate the impact of data revisions on business cycles and economic policy;
- Discussions of revisions to annual estimates of GDP and GDI and its major components;
- A look at the relationship of quarterly estimates of GDP and GDI and weighted averages of the two measures; and
- The conclusions of this analysis.
In table 1, the MARs to the annual rates of change of both current-dollar and real quarterly GDP growth—the average of the revisions without regard to sign from the current quarterly estimates to the latest estimates—range from 1.23 percentage points to 1.36 percentage points for 1996–2018. The MRs—the average allowing both positive and negative values for the revisions–range between −0.12 percentage point to 0.17 percentage point. MRs indicate whether the revisions are generally positive or negative. Because revisions may be offsetting, the MRs are much smaller than the MARs (see the box “Mean Revisions, Mean Absolute Revisions, and Standard Deviations”).
The MARs among the current quarterly estimates are smaller than the MARs from the current quarterly estimates to the latest estimates. For example, in table 2, the MAR from the advance estimates to the second estimates of real GDP is 0.50 percentage point, the MAR from the advance estimates to the third estimates is 0.63 percentage point, and the MAR from the second estimates to the third estimates is 0.28 percentage point.
In table B in the appendix, one can see, for example, that the MR for real GDP from the advance estimates to the latest estimates is just −0.01 percentage point, a tiny revision. The MRs from the second and third estimates to the latest estimates are −0.09 and −0.10 percentage point respectively, still rather small. To put these MRs into context for 1996–2018, the mean growth of real GDP (latest estimates) over this period was 2.50 percent, and the growth rates ranged from −8.38 percent to 7.53 percent.
Mean absolute revisions
Table 1 presents revisions for real and current-dollar GDP and their components. For all three current quarterly vintages for 1996–2018, the MARs for both current-dollar GDP and real GDP are somewhat larger than 1.20 percentage points. The MARs for current–dollar GDP are slightly larger than the MARs for real GDP for all current quarterly vintages. For current–dollar measures, the MARs decline slightly but steadily from the advance to the third estimates, while for real measures, the MARs stay constant and then decrease slightly from the advance to the third estimates. The decline in MARs with successive vintages is expected, as BEA receives and incorporates more and better source data with each vintage.
| Vintage | Mean absolute revision | Mean revision | Standard deviation | |||
|---|---|---|---|---|---|---|
| Current dollar | Real | Current dollar | Real | Current dollar | Real | |
| Gross domestic product | ||||||
| Advance | 1.36 | 1.26 | 0.17 | −0.01 | 1.66 | 1.59 |
| Second | 1.30 | 1.26 | 0.05 | −0.06 | 1.59 | 1.56 |
| Third | 1.29 | 1.23 | −0.03 | −0.12 | 1.58 | 1.51 |
| Personal consumption expenditures | ||||||
| Advance | 1.03 | 0.99 | −0.09 | −0.14 | 1.27 | 1.22 |
| Second | 0.92 | 0.90 | −0.07 | −0.13 | 1.16 | 1.12 |
| Third | 0.90 | 0.88 | −0.11 | −0.14 | 1.14 | 1.07 |
| Durable goods | ||||||
| Advance | 3.93 | 4.14 | −0.49 | −0.32 | 5.05 | 5.31 |
| Second | 3.93 | 4.06 | −0.39 | −0.24 | 4.96 | 5.18 |
| Third | 3.86 | 3.99 | −0.50 | −0.36 | 4.85 | 5.08 |
| Nondurable goods | ||||||
| Advance | 2.12 | 1.75 | −0.42 | −0.26 | 2.68 | 2.31 |
| Second | 1.98 | 1.64 | −0.43 | −0.25 | 2.45 | 2.23 |
| Third | 2.00 | 1.64 | −0.49 | −0.29 | 2.48 | 2.23 |
| Services | ||||||
| Advance | 0.95 | 0.91 | 0.05 | −0.10 | 1.21 | 1.15 |
| Second | 0.92 | 0.85 | 0.07 | −0.12 | 1.17 | 1.10 |
| Third | 0.82 | 0.79 | 0.05 | −0.10 | 1.00 | 0.99 |
| Gross private domestic investment | ||||||
| Advance | 4.40 | 4.54 | 0.97 | 0.62 | 5.98 | 6.35 |
| Second | 4.90 | 4.92 | 0.24 | 0.04 | 6.59 | 6.56 |
| Third | 4.75 | 4.69 | 0.15 | 0.02 | 6.33 | 6.26 |
| Fixed investment | ||||||
| Advance | 2.89 | 2.80 | 0.99 | 0.74 | 3.44 | 3.51 |
| Second | 2.59 | 2.59 | 0.40 | 0.18 | 3.33 | 3.31 |
| Third | 2.48 | 2.49 | 0.14 | 0.00 | 3.19 | 3.17 |
| Nonresidential | ||||||
| Advance | 3.53 | 3.44 | 0.86 | 0.81 | 4.20 | 4.27 |
| Second | 3.34 | 3.27 | 0.18 | 0.14 | 4.22 | 4.14 |
| Third | 3.17 | 3.11 | −0.02 | −0.03 | 4.05 | 3.94 |
| Structures | ||||||
| Advance | 8.58 | 7.74 | 3.42 | 2.16 | 10.32 | 9.78 |
| Second | 7.94 | 7.07 | 2.15 | 1.08 | 10.11 | 9.38 |
| Third | 7.57 | 6.54 | 1.42 | 0.62 | 9.69 | 8.59 |
| Equipment and intellectual property products | ||||||
| Advance | 3.69 | 4.54 | 0.24 | 0.55 | 4.54 | 5.67 |
| Second | 3.51 | 4.14 | −0.39 | −0.09 | 4.74 | 5.39 |
| Third | 3.30 | 4.06 | −0.44 | −0.12 | 4.55 | 5.38 |
| Residential | ||||||
| Advance | 4.00 | 3.75 | 1.04 | 0.11 | 4.59 | 4.69 |
| Second | 3.49 | 3.33 | 0.70 | −0.13 | 4.17 | 4.23 |
| Third | 3.21 | 3.11 | 0.31 | −0.33 | 3.90 | 3.98 |
| Change in private inventories1 | ||||||
| Net exports of goods and services1 | ||||||
| Exports | ||||||
| Advance | 3.35 | 3.26 | 0.73 | 0.85 | 4.75 | 4.20 |
| Second | 2.80 | 2.79 | 0.18 | 0.33 | 3.95 | 3.57 |
| Third | 2.80 | 2.80 | 0.06 | 0.22 | 3.73 | 3.39 |
| Imports | ||||||
| Advance | 3.68 | 3.36 | 0.44 | 0.75 | 4.81 | 4.40 |
| Second | 2.78 | 2.60 | 0.06 | 0.38 | 3.91 | 3.66 |
| Third | 2.76 | 2.61 | 0.17 | 0.50 | 3.76 | 3.57 |
| Government consumption expenditures and gross investment | ||||||
| Advance | 1.67 | 1.58 | 0.30 | −0.06 | 2.10 | 2.08 |
| Second | 1.69 | 1.64 | 0.22 | −0.06 | 2.10 | 2.16 |
| Third | 1.70 | 1.64 | 0.22 | −0.03 | 2.10 | 2.13 |
| Federal | ||||||
| Advance | 3.17 | 2.98 | −0.19 | −0.34 | 4.10 | 4.01 |
| Second | 3.10 | 2.99 | −0.22 | −0.27 | 3.99 | 4.01 |
| Third | 3.03 | 3.04 | −0.20 | −0.23 | 3.92 | 4.00 |
| Defense | ||||||
| Advance | 4.16 | 4.10 | −0.65 | −0.85 | 5.55 | 5.51 |
| Second | 4.20 | 4.04 | −0.65 | −0.72 | 5.54 | 5.54 |
| Third | 4.18 | 4.08 | −0.61 | −0.68 | 5.51 | 5.52 |
| Nondefense | ||||||
| Advance | 4.12 | 3.64 | 0.47 | 0.41 | 5.28 | 4.75 |
| Second | 4.27 | 3.76 | 0.36 | 0.33 | 5.43 | 5.05 |
| Third | 4.18 | 3.87 | 0.34 | 0.36 | 5.35 | 5.04 |
| State and local | ||||||
| Advance | 1.80 | 1.58 | 0.57 | 0.07 | 2.18 | 2.00 |
| Second | 1.64 | 1.50 | 0.46 | 0.03 | 2.11 | 1.94 |
| Third | 1.63 | 1.42 | 0.45 | 0.06 | 2.07 | 1.86 |
- Percent changes cannot be calculated due to the presence of both positive and negative values.
The MARs for current-dollar personal consumption expenditures (PCE) are about 0.30 percentage point smaller than those for the corresponding vintages of current-dollar GDP; the MARs are 1.03 percentage point for the advance estimates, 0.92 percentage point for the second estimate and 0.90 percentage point for the third estimate. Those for real PCE are slightly smaller at 0.99 percentage point, 0.90 percentage point, and 0.88 percentage point for the advance, second, and third vintages, respectively. MARs for both current-dollar and real measures tend to decline slightly with successive vintages.
Within PCE, the MARs for durable goods are noticeably larger, about 3.93 percentage points for current-dollar durable goods and 4.14 percentage points for real durable goods. Also notable is that durable goods is the only category within PCE in which the MARs are larger for the real measure than for the current-dollar measure.
The MARs for nondurable goods are larger than those for all PCE and tend to decline with successive vintages of estimates. The MARs for the advance estimate is 2.12 percentage points, and those for the second and third estimates are close to 2.00 percentage points. The MARs for the real estimates are approximately 0.35 percentage point smaller than those for current-dollar estimates.
The MARs for services are the smallest of all PCE components shown. The MARs for current-dollar services are 0.95 percentage points for the advance, 0.92 for the second estimates, and 0.82 percentage point for the third estimate. The MARs for the corresponding real estimates are slightly smaller, but the differences are less than 0.10 percentage point. Moreover, the MARs for services decline with successive vintages.
The MARs for gross private domestic investment are relatively large; they range from around 4.40 percentage points to 4.92 percentage points for both current-dollar and real investment. Both increase by approximately half a percentage point from the advance estimate to the second estimates, then decrease by a quarter of a percentage point with the third estimate. The MARs for fixed investment are smaller; for current dollars and real estimates, the advance estimates are approximately 2.85 percentage points and the second and third estimates decrease by approximately 0.3 and 0.2 percentage point, respectively. The smaller sizes are the result of excluding inventory investment, which in a previous study using an alternative methodology, was found to have larger revisions (see Fixler, Greenaway-McGreevey, and Grimm (2011).
Within fixed investment, MARs for current-dollar nonresidential range from 3.17 percentage points to 3.53 percentage points, while real nonresidential MARs increase from 3.11 percentage points to 3.44 percentage points from the advance estimate to the third estimate. Additionally, MARs for current-dollar structures decrease from 8.58 percentage points for the advance estimates to 7.94 percentage points for the second estimates and 7.57 percent for the third estimates. MARs for real structures are slightly lower, decreasing from 7.74 percentage points for the advance to 7.07 percentage points for the second estimates and 6.54 percentage points for the third estimate.
In the category equipment and intellectual property products, MARs for the current-dollar revisions range from 3.30 percentage points to 3.69 percentage points over the three vintages and decrease from the advance estimate to the third estimate. MARs for the real estimates are slightly higher and range from 4.06 percentage points to 4.54 percentage points, again decreasing from the advance estimate to the third estimate.
The MARs for residential investment are in general approximately within the same range as those for equipment and intellectual property products investment. These estimates decline across successive vintages for both current-dollar estimates and real estimates.
The MARs for current-dollar estimates of exports and imports for the three current quarterly vintages range from 2.76 percentage points to 3.68 percentage points. The MARs for the corresponding real estimates tend to be slightly smaller, with very small differences for each vintage.
The MARs for government consumption expenditures and gross investment hover around 1.60 percentage points for all vintages. The MARs for federal expenditures for current-dollar estimates and real estimates are higher. They range from 2.98 to 3.17 percentage points; these estimates are relatively constant across all three vintages. The MARs for defense range from 4.16 percentage points to 4.20 percentage points in current dollars and from 4.04 percentage points to 4.10 percentage points in real dollars. Finally, the MARs for nondefense spending increases slightly across the three vintages for real estimates from 3.64 percentage to 3.87 percentage points, and current-dollar estimates hover around 4.20 percentage points. Finally, the MARs for state and local government expenditures for the current-dollar advance estimate is 1.80 percentage points and around 1.63 percentage points for both the second and third estimates. The MARs for the real estimates decrease across vintages, from 1.58 percentage points for the advance estimate to 1.42 percentage points for the third estimate.
Tables 2 and 3 present expanded information about the MARs of real and current-dollar GDP, including MARs for all vintages of estimates to any later estimate.
| Vintage | Vintage of revision used as standard | |||||
|---|---|---|---|---|---|---|
| Second | Third | Annual | Latest | |||
| First | Second | Third | ||||
| Gross domestic product | ||||||
| Advance | 0.50 | 0.63 | 0.91 | 1.07 | 1.23 | 1.36 |
| Second | 0.28 | 0.75 | 0.97 | 1.16 | 1.30 | |
| Third | 0.75 | 0.97 | 1.14 | 1.29 | ||
| First annual | 0.64 | 0.80 | 1.01 | |||
| Second annual | 0.48 | 0.87 | ||||
| Third annual | 0.69 | |||||
| Personal consumption expenditures | ||||||
| Advance | 0.28 | 0.41 | 0.72 | 0.86 | 0.92 | 1.03 |
| Second | 0.26 | 0.61 | 0.74 | 0.83 | 0.92 | |
| Third | 0.57 | 0.73 | 0.85 | 0.90 | ||
| First annual | 0.52 | 0.65 | 0.74 | |||
| Second annual | 0.45 | 0.61 | ||||
| Third annual | 0.58 | |||||
| Durables | ||||||
| Advance | 1.05 | 1.08 | 2.73 | 3.30 | 3.55 | 3.93 |
| Second | 0.34 | 2.40 | 3.10 | 3.64 | 3.93 | |
| Third | 2.52 | 3.13 | 3.56 | 3.86 | ||
| First annual | 2.17 | 2.49 | 2.92 | |||
| Second annual | 1.77 | 2.40 | ||||
| Third annual | 1.58 | |||||
| Nondurables | ||||||
| Advance | 0.58 | 0.62 | 1.20 | 1.70 | 1.98 | 2.12 |
| Second | 0.25 | 1.01 | 1.56 | 1.84 | 1.98 | |
| Third | 1.01 | 1.59 | 1.90 | 2.00 | ||
| First annual | 1.09 | 1.41 | 1.71 | |||
| Second annual | 0.80 | 1.35 | ||||
| Third annual | 1.16 | |||||
| Services | ||||||
| Advance | 0.26 | 0.49 | 0.76 | 0.97 | 0.98 | 0.95 |
| Second | 0.38 | 0.72 | 0.91 | 0.95 | 0.92 | |
| Third | 0.58 | 0.77 | 0.79 | 0.82 | ||
| First annual | 0.51 | 0.66 | 0.69 | |||
| Second annual | 0.47 | 0.71 | ||||
| Third annual | 0.62 | |||||
| Gross private domestic investment | ||||||
| Advance | 2.60 | 2.91 | 4.50 | 4.80 | 5.11 | 4.40 |
| Second | 0.99 | 3.98 | 4.63 | 5.28 | 4.90 | |
| Third | 3.80 | 4.39 | 5.12 | 4.75 | ||
| First annual | 2.85 | 3.66 | 3.81 | |||
| Second annual | 2.57 | 3.08 | ||||
| Third annual | 2.44 | |||||
| Fixed investment | ||||||
| Advance | 1.17 | 1.48 | 2.31 | 2.66 | 3.04 | 2.89 |
| Second | 0.66 | 1.98 | 2.45 | 2.81 | 2.59 | |
| Third | 1.82 | 2.35 | 2.63 | 2.48 | ||
| First annual | 1.84 | 2.24 | 2.25 | |||
| Second annual | 1.34 | 1.71 | ||||
| Third annual | 1.64 | |||||
| Fixed nonresidential investment | ||||||
| Advance | 1.48 | 1.75 | 2.81 | 3.42 | 3.79 | 3.53 |
| Second | 0.75 | 2.53 | 3.28 | 3.60 | 3.34 | |
| Third | 2.35 | 3.12 | 3.37 | 3.17 | ||
| First annual | 2.36 | 2.76 | 2.58 | |||
| Second annual | 1.67 | 2.17 | ||||
| Third annual | 2.01 | |||||
| Nonresidential structures invesment | ||||||
| Advance | 3.70 | 4.39 | 6.81 | 8.43 | 8.97 | 8.58 |
| Second | 2.01 | 6.54 | 7.70 | 8.34 | 7.94 | |
| Third | 6.12 | 7.16 | 8.16 | 7.57 | ||
| First annual | 4.73 | 5.53 | 5.73 | |||
| Second annual | 2.82 | 3.86 | ||||
| Third annual | 2.93 | |||||
| Equipment and intellectual property investment | ||||||
| Advance | 1.62 | 1.93 | 3.05 | 3.29 | 3.63 | 3.69 |
| Second | 0.77 | 2.64 | 3.48 | 3.71 | 3.51 | |
| Third | 2.48 | 3.23 | 3.62 | 3.30 | ||
| First annual | 2.71 | 3.10 | 3.13 | |||
| Second annual | 2.11 | 2.54 | ||||
| Third annual | 2.21 | |||||
| Residential investment | ||||||
| Advance | 1.24 | 1.66 | 3.32 | 3.74 | 4.03 | 4.00 |
| Second | 0.78 | 2.82 | 3.35 | 3.54 | 3.49 | |
| Third | 2.49 | 3.07 | 3.12 | 3.21 | ||
| First annual | 2.11 | 2.53 | 2.92 | |||
| Second annual | 1.39 | 2.10 | ||||
| Third annual | 1.48 | |||||
| Exports | ||||||
| Advance | 1.68 | 2.03 | 2.74 | 3.20 | 3.30 | 3.35 |
| Second | 0.97 | 2.16 | 2.48 | 2.80 | 2.80 | |
| Third | 2.10 | 2.43 | 2.71 | 2.80 | ||
| First annual | 1.66 | 2.02 | 2.22 | |||
| Second annual | 1.11 | 1.48 | ||||
| Third annual | 0.98 | |||||
| Imports | ||||||
| Advance | 1.89 | 2.12 | 2.87 | 3.54 | 3.70 | 3.68 |
| Second | 0.88 | 2.24 | 2.70 | 2.69 | 2.78 | |
| Third | 2.06 | 2.59 | 2.55 | 2.76 | ||
| First annual | 1.83 | 2.00 | 2.30 | |||
| Second annual | 1.09 | 1.58 | ||||
| Third annual | 1.24 | |||||
| Government consumption expenditures and gross investment | ||||||
| Advance | 0.52 | 0.61 | 1.14 | 1.22 | 1.62 | 1.67 |
| Second | 0.24 | 1.00 | 1.14 | 1.55 | 1.69 | |
| Third | 1.01 | 1.15 | 1.56 | 1.70 | ||
| First annual | 0.79 | 1.24 | 1.68 | |||
| Second annual | 0.88 | 1.46 | ||||
| Third annual | 1.42 | |||||
| Federal government | ||||||
| Advance | 0.55 | 0.53 | 2.17 | 2.39 | 2.98 | 3.17 |
| Second | 0.20 | 2.03 | 2.26 | 2.92 | 3.10 | |
| Third | 2.09 | 2.32 | 2.98 | 3.03 | ||
| First annual | 1.38 | 2.12 | 3.01 | |||
| Second annual | 1.30 | 2.73 | ||||
| Third annual | 2.88 | |||||
| Federal defense | ||||||
| Advance | 0.65 | 0.68 | 2.29 | 2.85 | 3.60 | 4.16 |
| Second | 0.18 | 2.28 | 2.78 | 3.58 | 4.20 | |
| Third | 2.28 | 2.78 | 3.59 | 4.18 | ||
| First annual | 1.56 | 2.39 | 3.87 | |||
| Second annual | 1.39 | 3.83 | ||||
| Third annual | 3.82 | |||||
| Federal nondefense | ||||||
| Advance | 0.75 | 0.72 | 3.70 | 3.96 | 4.47 | 4.12 |
| Second | 0.31 | 3.78 | 3.99 | 4.27 | 4.27 | |
| Third | 3.74 | 3.93 | 4.32 | 4.18 | ||
| First annual | 2.24 | 3.03 | 3.69 | |||
| Second annual | 1.90 | 3.19 | ||||
| Third annual | 4.12 | |||||
| State and local government | ||||||
| Advance | 0.70 | 0.82 | 1.17 | 1.41 | 1.70 | 1.80 |
| Second | 0.33 | 0.96 | 1.32 | 1.54 | 1.64 | |
| Third | 0.94 | 1.24 | 1.54 | 1.63 | ||
| First annual | 0.81 | 1.28 | 1.53 | |||
| Second annual | 1.06 | 1.35 | ||||
| Third annual | 1.34 | |||||
Table 2 shows that the MARs for the various vintages of current-dollar estimates all increase with later vintages. Specifically, the increase in MARs is largest from earlier current quarterly estimates to the first annual estimate. The increase in MARs tapers off following the first annual estimate. The reason for the large jump in MARs from earlier estimates to the first annual estimate is that comprehensive revisions of the NIPAs are made in 5-year intervals; as a result, the first annual revision estimates contain the redefinitions and reclassifications about one-fifth of the time; the second annual revision estimates, about two-fifths of the time; and the third annual revision estimates, about three-fifths of the time. Thus, the MARs for the successive annual revision estimates increasingly reflect the effects of these changes as well as the incorporation of annual data that become available with 1- to 3-year lags.
These same patterns generally hold true for the major components and subcomponents of current-dollar GDP. The MARs for PCE tend to be modestly lower than those for GDP. The MARs for durables PCE are the largest among the subcomponents of total PCE. In fact, they are several times larger than the MARs for total PCE. MARs for nondurables PCE are almost twice the MARs of PCE but smaller than the MARs for durable goods. The MARs for services PCE is comparable to that of total PCE.
The MARs for gross private domestic investment are substantially larger than the MARs for all other components of GDP and about 5 times as large as the MARs for current-dollar GDP. The MARs for fixed investment are about half of the corresponding MARs for gross private domestic investment; the differences reflect the exclusion of change in private inventories, which are subject to large unmeasurable (in percent changes) revisions. Within fixed nonresidential investment, the MARs for nonresidential structures investment is about twice as much as the MARs for equipment and intellectual property investment. For residential investment, the size of the MARs are comparable to those for nonresidential investment. However, the MARs for residential investment from the earlier vintages to the first annual estimates and beyond are larger than those for nonresidential investment.
For exports and imports, the patterns of MARs are roughly the same and similar to the patterns for the other components of GDP, with the MARs of the advance estimate to later vintages of imports estimates being just slightly larger than those for exports.
The patterns of MARs for government consumption expenditures and gross investment are also similar to those for GDP, though slightly larger. The patterns of MARs for the components and subcomponents of government are roughly similar to the aggregate but with slightly larger values, particularly for federal nondefense, and the first two estimates of state and local government. The later MARs estimates for state and local government are smaller than the MARs of other government components and more similar in size to the MARs for the government consumption expenditures and gross investment aggregate. Relatively little new information comes in for the later estimates, and the sizes of the revisions reflect this fact.
In summary, there are several characteristics of the pattern of revisions that hold true generally but not universally. The difference in revisions from the second to the third vintages of estimates are typically the smallest for most adjacent pair of vintages. For any given vintage, the MARs tend to increase as later and later vintages include more comprehensive revisions. For any vintage of later estimates, the MARs tend to decrease in size as later and later vintages of estimates are used as the earlier estimates that have already incorporated a lot of information. That is, for any row (vintage of earlier estimates) in table 2, moving across columns of later and later estimates results in increasingly large MARs. Also, for any given column (vintage of later estimates), going down rows generally results in decreasing MARs.
Table 3 presents MARs for real GDP and its components. Both the sizes and the patterns of the MARs are close to those of MARs for current-dollar GDP. The similarities reflect the fact that revisions to deflators used to construct the real estimates are quite small in comparison to the current-dollar revisions, and most estimates of the components of GDP are made in current dollars and then deflated.
| Vintage | Vintage of revision used as standard | |||||
|---|---|---|---|---|---|---|
| Second | Third | Annual | Latest | |||
| First | Second | Third | ||||
| Gross domestic product | ||||||
| Advance | 0.53 | 0.59 | 0.88 | 0.96 | 1.19 | 1.26 |
| Second | 0.28 | 0.77 | 0.95 | 1.17 | 1.26 | |
| Third | 0.77 | 0.94 | 1.15 | 1.23 | ||
| First annual | 0.65 | 0.84 | 1.01 | |||
| Second annual | 0.57 | 0.88 | ||||
| Third annual | 0.56 | |||||
| Personal consumption expenditures | ||||||
| Advance | 0.28 | 0.39 | 0.73 | 0.82 | 0.92 | 0.99 |
| Second | 0.24 | 0.63 | 0.74 | 0.82 | 0.90 | |
| Third | 0.60 | 0.72 | 0.78 | 0.88 | ||
| First annual | 0.50 | 0.60 | 0.69 | |||
| Second annual | 0.41 | 0.55 | ||||
| Third annual | 0.41 | |||||
| Durables | ||||||
| Advance | 1.08 | 1.11 | 2.86 | 3.44 | 3.73 | 4.14 |
| Second | 0.36 | 2.53 | 3.22 | 3.75 | 4.06 | |
| Third | 2.65 | 3.21 | 3.67 | 3.99 | ||
| First annual | 2.23 | 2.62 | 2.97 | |||
| Second annual | 1.90 | 2.46 | ||||
| Third annual | 1.60 | |||||
| Nondurables | ||||||
| Advance | 0.58 | 0.63 | 1.06 | 1.37 | 1.48 | 1.75 |
| Second | 0.25 | 0.97 | 1.31 | 1.40 | 1.64 | |
| Third | 0.93 | 1.30 | 1.41 | 1.64 | ||
| First annual | 0.91 | 1.10 | 1.41 | |||
| Second annual | 0.68 | 1.08 | ||||
| Third annual | 0.83 | |||||
| Services | ||||||
| Advance | 0.24 | 0.47 | 0.74 | 0.93 | 0.91 | 0.91 |
| Second | 0.35 | 0.69 | 0.87 | 0.87 | 0.85 | |
| Third | 0.58 | 0.74 | 0.75 | 0.79 | ||
| First annual | 0.49 | 0.63 | 0.68 | |||
| Second annual | 0.49 | 0.69 | ||||
| Third annual | 0.54 | |||||
| Gross private domestic investment | ||||||
| Advance | 2.52 | 2.77 | 4.74 | 4.87 | 5.21 | 4.54 |
| Second | 0.97 | 4.15 | 4.59 | 5.31 | 4.92 | |
| Third | 3.98 | 4.28 | 5.15 | 4.69 | ||
| First annual | 3.05 | 3.90 | 4.14 | |||
| Second annual | 2.63 | 3.39 | ||||
| Third annual | 2.56 | |||||
| Fixed investment | ||||||
| Advance | 1.11 | 1.40 | 2.31 | 2.73 | 3.03 | 2.80 |
| Second | 0.65 | 2.02 | 2.50 | 2.85 | 2.59 | |
| Third | 1.89 | 2.41 | 2.71 | 2.49 | ||
| First annual | 1.87 | 2.27 | 2.22 | |||
| Second annual | 1.34 | 1.73 | ||||
| Third annual | 1.48 | |||||
| Fixed nonresidential investment | ||||||
| Advance | 1.46 | 1.71 | 2.87 | 3.43 | 3.74 | 3.44 |
| Second | 0.76 | 2.54 | 3.24 | 3.54 | 3.27 | |
| Third | 2.38 | 3.08 | 3.32 | 3.11 | ||
| First annual | 2.41 | 2.82 | 2.69 | |||
| Second annual | 1.69 | 2.12 | ||||
| Third annual | 1.86 | |||||
| Nonresidential structures invesment | ||||||
| Advance | 3.52 | 4.22 | 6.75 | 7.76 | 8.14 | 7.74 |
| Second | 2.11 | 6.65 | 7.23 | 7.41 | 7.07 | |
| Third | 5.97 | 6.55 | 7.02 | 6.54 | ||
| First annual | 4.43 | 4.84 | 5.28 | |||
| Second annual | 2.53 | 3.35 | ||||
| Third annual | 2.34 | |||||
| Equipment and intellectual property investment | ||||||
| Advance | 1.68 | 1.83 | 3.24 | 3.63 | 4.32 | 4.54 |
| Second | 0.70 | 2.87 | 3.88 | 4.26 | 4.14 | |
| Third | 2.73 | 3.66 | 4.19 | 4.06 | ||
| First annual | 2.95 | 3.59 | 3.86 | |||
| Second annual | 2.87 | 3.51 | ||||
| Third annual | 2.31 | |||||
| Residential investment | ||||||
| Advance | 1.32 | 1.65 | 3.28 | 4.08 | 3.71 | 3.75 |
| Second | 0.77 | 2.79 | 3.76 | 3.36 | 3.33 | |
| Third | 2.50 | 3.54 | 3.07 | 3.11 | ||
| First annual | 2.86 | 2.89 | 3.10 | |||
| Second annual | 1.90 | 2.59 | ||||
| Third annual | 1.30 | |||||
| Exports | ||||||
| Advance | 1.60 | 1.99 | 2.66 | 3.00 | 3.15 | 3.26 |
| Second | 0.95 | 2.15 | 2.47 | 2.72 | 2.79 | |
| Third | 2.09 | 2.40 | 2.66 | 2.80 | ||
| First annual | 1.56 | 1.90 | 2.21 | |||
| Second annual | 1.07 | 1.50 | ||||
| Third annual | 0.93 | |||||
| Imports | ||||||
| Advance | 1.83 | 2.06 | 3.01 | 3.28 | 3.55 | 3.36 |
| Second | 0.83 | 2.28 | 2.56 | 2.68 | 2.60 | |
| Third | 2.17 | 2.46 | 2.52 | 2.61 | ||
| First annual | 1.77 | 2.02 | 2.17 | |||
| Second annual | 1.37 | 1.79 | ||||
| Third annual | 1.53 | |||||
| Government consumption expenditures and gross investment | ||||||
| Advance | 0.52 | 0.57 | 0.99 | 1.21 | 1.56 | 1.58 |
| Second | 0.23 | 0.89 | 1.17 | 1.56 | 1.64 | |
| Third | 0.83 | 1.16 | 1.58 | 1.64 | ||
| First annual | 0.78 | 1.21 | 1.39 | |||
| Second annual | 0.87 | 1.29 | ||||
| Third annual | 1.14 | |||||
| Federal government | ||||||
| Advance | 0.58 | 0.55 | 1.94 | 2.23 | 2.89 | 2.98 |
| Second | 0.22 | 1.74 | 2.11 | 2.83 | 2.99 | |
| Third | 1.78 | 2.14 | 2.88 | 3.04 | ||
| First annual | 1.38 | 2.07 | 2.82 | |||
| Second annual | 1.37 | 2.66 | ||||
| Third annual | 2.52 | |||||
| Federal defense | ||||||
| Advance | 0.69 | 0.74 | 2.32 | 3.31 | 3.24 | 4.10 |
| Second | 0.22 | 2.12 | 3.17 | 3.16 | 4.04 | |
| Third | 2.17 | 3.18 | 3.15 | 4.08 | ||
| First annual | 2.54 | 2.79 | 3.93 | |||
| Second annual | 2.13 | 4.24 | ||||
| Third annual | 3.29 | |||||
| Federal nondefense | ||||||
| Advance | 0.77 | 0.73 | 3.41 | 3.70 | 4.11 | 3.64 |
| Second | 0.32 | 3.50 | 3.81 | 4.05 | 3.76 | |
| Third | 3.50 | 3.77 | 4.10 | 3.87 | ||
| First annual | 2.02 | 2.59 | 3.16 | |||
| Second annual | 1.63 | 2.72 | ||||
| Third annual | 3.40 | |||||
| State and local government | ||||||
| Advance | 0.67 | 0.78 | 1.34 | 1.34 | 1.66 | 1.58 |
| Second | 0.34 | 1.24 | 1.26 | 1.54 | 1.50 | |
| Third | 1.12 | 1.15 | 1.50 | 1.42 | ||
| First annual | 1.16 | 1.63 | 1.66 | |||
| Second annual | 1.03 | 1.02 | ||||
| Third annual | 0.85 | |||||
Table 4 provides additional information about the revisions from earlier vintages of estimates to the latest estimates. Columns 1 and 2 show the standard deviations of the latest estimates of real and current-dollar GDP and its components and subcomponents at the same level of detail as in table 1 and table 2. These are measures of the volatility of the estimates. They range from 1.47 percentage points for real PCE services to 15.48 percentage points for current-dollar structures investment.
| Vintage | Standard deviation of estimates | Standard deviation of revisions | Scaled standard deviation | |||
|---|---|---|---|---|---|---|
| Current-dollar | Real | Current-dollar | Real | Current-dollar | Real | |
| Gross domestic product | 2.70 | 2.42 | ||||
| Advance | 1.66 | 1.59 | 0.61 | 0.66 | ||
| Second | 1.59 | 1.56 | 0.59 | 0.64 | ||
| Third | 1.58 | 1.51 | 0.58 | 0.62 | ||
| First annual | 1.27 | 1.27 | 0.47 | 0.53 | ||
| Second annual | 1.11 | 1.11 | 0.41 | 0.46 | ||
| Third annual | 0.90 | 0.77 | 0.33 | 0.32 | ||
| Personal consumption expenditures | 2.57 | 1.98 | ||||
| Advance | 1.27 | 1.22 | 0.49 | 0.62 | ||
| Second | 1.16 | 1.12 | 0.45 | 0.56 | ||
| Third | 1.14 | 1.07 | 0.44 | 0.54 | ||
| First annual | 0.93 | 0.92 | 0.36 | 0.46 | ||
| Second annual | 0.76 | 0.69 | 0.29 | 0.35 | ||
| Third annual | 0.70 | 0.61 | 0.27 | 0.31 | ||
| Durable goods | 8.32 | 8.69 | ||||
| Advance | 5.05 | 5.31 | 0.61 | 0.61 | ||
| Second | 4.96 | 5.18 | 0.60 | 0.60 | ||
| Third | 4.85 | 5.08 | 0.58 | 0.58 | ||
| First annual | 3.86 | 3.92 | 0.46 | 0.45 | ||
| Second annual | 3.38 | 3.43 | 0.41 | 0.40 | ||
| Third annual | 2.22 | 2.82 | 0.27 | 0.32 | ||
| Nondurable goods | 5.37 | 2.53 | ||||
| Advance | 2.68 | 2.31 | 0.50 | 0.91 | ||
| Second | 2.45 | 2.23 | 0.46 | 0.88 | ||
| Third | 2.48 | 2.23 | 0.46 | 0.88 | ||
| First annual | 2.25 | 1.86 | 0.42 | 0.73 | ||
| Second annual | 1.72 | 1.38 | 0.32 | 0.55 | ||
| Third annual | 1.45 | 1.20 | 0.27 | 0.47 | ||
| Services | 1.86 | 1.47 | ||||
| Advance | 1.21 | 1.15 | 0.65 | 0.78 | ||
| Second | 1.17 | 1.10 | 0.63 | 0.75 | ||
| Third | 1.00 | 0.99 | 0.54 | 0.67 | ||
| First annual | 0.88 | 0.86 | 0.47 | 0.59 | ||
| Second annual | 0.88 | 0.86 | 0.47 | 0.59 | ||
| Third annual | 0.82 | 0.76 | 0.44 | 0.52 | ||
| Gross private domestic investment | 12.07 | 12.07 | ||||
| Advance | 5.98 | 6.35 | 0.50 | 0.53 | ||
| Second | 6.59 | 6.56 | 0.55 | 0.54 | ||
| Third | 6.33 | 6.26 | 0.52 | 0.52 | ||
| First annual | 5.40 | 5.84 | 0.45 | 0.48 | ||
| Second annual | 4.13 | 4.47 | 0.34 | 0.37 | ||
| Third annual | 3.18 | 3.58 | 0.26 | 0.30 | ||
| Fixed investment | 7.85 | 7.39 | ||||
| Advance | 3.44 | 3.51 | 0.44 | 0.48 | ||
| Second | 3.33 | 3.31 | 0.42 | 0.45 | ||
| Third | 3.19 | 3.17 | 0.41 | 0.43 | ||
| First annual | 2.95 | 2.96 | 0.38 | 0.40 | ||
| Second annual | 2.07 | 2.05 | 0.26 | 0.28 | ||
| Third annual | 2.09 | 2.13 | 0.27 | 0.29 | ||
| Fixed nonresidential investment | 8.05 | 7.68 | ||||
| Advance | 4.20 | 4.27 | 0.52 | 0.56 | ||
| Second | 4.22 | 4.14 | 0.52 | 0.54 | ||
| Third | 4.05 | 3.94 | 0.50 | 0.51 | ||
| First annual | 3.61 | 3.63 | 0.45 | 0.47 | ||
| Second annual | 2.62 | 2.53 | 0.33 | 0.33 | ||
| Third annual | 2.54 | 2.64 | 0.32 | 0.34 | ||
| Structures investment | 15.48 | 13.38 | ||||
| Advance | 10.32 | 9.78 | 0.67 | 0.73 | ||
| Second | 10.11 | 9.38 | 0.65 | 0.70 | ||
| Third | 9.69 | 8.59 | 0.63 | 0.64 | ||
| First annual | 7.50 | 6.80 | 0.48 | 0.51 | ||
| Second annual | 4.73 | 4.35 | 0.31 | 0.33 | ||
| Third annual | 3.80 | 3.40 | 0.25 | 0.25 | ||
| Equipment and intellectual property products | 7.75 | 11.36 | ||||
| Advance | 4.54 | 5.67 | 0.59 | 0.50 | ||
| Second | 4.74 | 5.39 | 0.61 | 0.47 | ||
| Third | 4.55 | 5.38 | 0.59 | 0.47 | ||
| First annual | 4.40 | 5.19 | 0.57 | 0.46 | ||
| Second annual | 3.00 | 4.88 | 0.39 | 0.43 | ||
| Third annual | 2.83 | 3.67 | 0.36 | 0.32 | ||
| Residential investment | 14.24 | 12.91 | ||||
| Advance | 4.59 | 4.69 | 0.32 | 0.36 | ||
| Second | 4.17 | 4.23 | 0.29 | 0.33 | ||
| Third | 3.90 | 3.98 | 0.27 | 0.31 | ||
| First annual | 3.72 | 4.49 | 0.26 | 0.35 | ||
| Second annual | 2.76 | 3.67 | 0.19 | 0.28 | ||
| Third annual | 1.97 | 1.87 | 0.14 | 0.14 | ||
| Net exports of goods and services | ||||||
| Exports | 11.42 | 8.61 | ||||
| Advance | 4.75 | 4.20 | 0.42 | 0.49 | ||
| Second | 3.95 | 3.57 | 0.35 | 0.41 | ||
| Third | 3.73 | 3.39 | 0.33 | 0.39 | ||
| First annual | 2.98 | 2.84 | 0.26 | 0.33 | ||
| Second annual | 1.98 | 1.97 | 0.17 | 0.23 | ||
| Third annual | 1.44 | 1.53 | 0.13 | 0.18 | ||
| Imports | 12.84 | 8.33 | ||||
| Advance | 4.81 | 4.40 | 0.37 | 0.53 | ||
| Second | 3.91 | 3.66 | 0.30 | 0.44 | ||
| Third | 3.76 | 3.57 | 0.29 | 0.43 | ||
| First annual | 3.31 | 2.98 | 0.26 | 0.36 | ||
| Second annual | 2.12 | 2.43 | 0.17 | 0.29 | ||
| Third annual | 1.72 | 2.14 | 0.13 | 0.26 | ||
| Government consumption expenditures and gross investment | 3.25 | 2.73 | ||||
| Advance | 2.10 | 2.08 | 0.65 | 0.76 | ||
| Second | 2.10 | 2.16 | 0.65 | 0.79 | ||
| Third | 2.10 | 2.13 | 0.65 | 0.78 | ||
| First annual | 2.00 | 1.83 | 0.61 | 0.67 | ||
| Second annual | 1.82 | 1.65 | 0.56 | 0.60 | ||
| Third annual | 1.82 | 1.58 | 0.56 | 0.58 | ||
| Federal | 5.97 | 5.30 | ||||
| Advance | 4.10 | 4.01 | 0.69 | 0.76 | ||
| Second | 3.99 | 4.01 | 0.67 | 0.76 | ||
| Third | 3.92 | 4.00 | 0.66 | 0.76 | ||
| First annual | 3.83 | 3.74 | 0.64 | 0.71 | ||
| Second annual | 3.54 | 3.47 | 0.59 | 0.66 | ||
| Third annual | 3.65 | 3.48 | 0.61 | 0.66 | ||
| Defense | 8.07 | 7.15 | ||||
| Advance | 5.55 | 5.51 | 0.69 | 0.77 | ||
| Second | 5.54 | 5.54 | 0.69 | 0.77 | ||
| Third | 5.51 | 5.52 | 0.68 | 0.77 | ||
| First annual | 4.99 | 5.20 | 0.62 | 0.73 | ||
| Second annual | 4.91 | 5.78 | 0.61 | 0.81 | ||
| Third annual | 4.84 | 4.95 | 0.60 | 0.69 | ||
| Nondefense | 5.67 | 5.81 | ||||
| Advance | 5.28 | 4.75 | 0.93 | 0.82 | ||
| Second | 5.43 | 5.05 | 0.96 | 0.87 | ||
| Third | 5.35 | 5.04 | 0.94 | 0.87 | ||
| First annual | 4.99 | 4.22 | 0.88 | 0.73 | ||
| Second annual | 4.58 | 3.89 | 0.81 | 0.67 | ||
| Third annual | 5.59 | 4.62 | 0.99 | 0.79 | ||
| State and local | 3.24 | 2.73 | ||||
| Advance | 2.18 | 2.00 | 0.67 | 0.73 | ||
| Second | 2.11 | 1.94 | 0.65 | 0.71 | ||
| Third | 2.07 | 1.86 | 0.64 | 0.68 | ||
| First annual | 1.87 | 3.36 | 0.58 | 1.23 | ||
| Second annual | 1.69 | 1.40 | 0.52 | 0.51 | ||
| Third annual | 1.74 | 1.32 | 0.54 | 0.48 | ||
Columns 3 and 4 of table 4 expand upon columns 5 and 6 of table 1 by presenting standard deviations of the three annual revision vintages of estimates. Again, the standard deviations show wide variation in size, ranging from 0.70 percentage point for current-dollar PCE and 0.61 percentage point for real PCE to 10.32 percentage points for current-dollar structures investment and 9.78 percentage points for real structures investment. The standard deviations may be scaled by dividing the standard deviations of the revisions by the standard deviation of the estimates in order to facilitate comparisons among components. When the standard deviations of revisions are scaled, the resulting standard deviations for each component and subcomponent have relatively small ranges. from 0.13 percentage point (imports) to 0.99 percentage point (federal nondefense) for current-dollar GDP and 0.14 percentage point (residential investment) to 1.23 percentage points (state and local) for real GDP. Thus, the more volatile components of GDP (those with larger standard deviation of estimates) also tend to have more variable revisions (larger standard deviation of revisions).
Mean revisions
In addition to MARs, table 1 presents MRs for real and current-dollar GDP. The reported MRs are generally much smaller than the MARs because positive and negative revisions tend to offset each other, and MARs are functions of both the MRs and the variances of the estimates, which by definition are positive. For most of the measures shown in table 1, there is little or no tendency for MRs to become smaller with successive vintages of estimates. Most of the MRs for GDP and its components reflect definitional changes that are part of comprehensive revisions made to improve the estimates, and these revisions have usually raised the rates of change of GDP and some components.
The MRs for both current-dollar and real GDP are generally negative. The MR for the advance estimates of current-dollar GDP is 0.17 percentage point, and the MR for real GDP is −0.01 percentage point. The MRs for the second and third current-dollar estimates of GDP are 0.05 percentage point and −0.03 percentage point, respectively, and the corresponding MRs for real GDP are −0.06 percentage point and −0.12 percentage point, respectively. The MRs for the components and subcomponents of real and current-dollar GDP are generally small, except for the MRs of current-dollar structures investment, which are substantially larger. The signs of the MRs vary across subcomponents and often vary with successive vintages.
Table 1 also presents the standard deviations of revisions. They are somewhat larger than the MARs for GDP and its components. The pattern observed for the MARs discussed in the previous section holds true in general for the standard deviations as well. For example, within PCE, durables have the largest standard deviations while services have the smallest. Also, the largest standard deviations are observed for gross private domestic investment.
The standard deviations in table 1 can be used to test whether the MRs are statistically significant.3 The revisions that underlie the reported MRs appear to be normally distributed, and the MRs are not statistically different than zero for GDP or any of its components or subcomponents. This is true for current-dollar as well as real GDP.
Tables 5 and 6 offer supplemental pictures of the revisions. Table 5 focuses on the advance to latest estimate of real GDP and its major components, providing additional information about the distribution of the revisions. In table 5, the number and proportion of observations that fall within the 1 standard deviation range of the MRs are reported. The revisions appear to hover around the mean and the proportions approximate what one would observe for normally distributed random variables.
| Component | Percent | Number of observations within 1 standard deviation | Percent of observations within 1 standard deviation | ||
|---|---|---|---|---|---|
| Minus 1 standard deviation | Mean | Plus 1 standard deviation | |||
| Gross domestic product | −1.54 | −0.07 | 1.54 | 67 | 73 |
| Personal consumption expenditure | −1.18 | −0.11 | 1.18 | 60 | 65 |
| Gross private domestic investment | −6.67 | −0.35 | 6.67 | 64 | 70 |
| Net exports of goods and services | |||||
| Exports | −3.36 | 0.85 | 5.05 | 65 | 71 |
| Imports | −3.65 | 0.75 | 5.15 | 66 | 72 |
| Government consumption expenditures and gross investment | |||||
| Federal | −4.35 | −0.34 | 3.67 | 67 | 73 |
| State and local | −1.94 | 0.07 | 2.07 | 68 | 74 |
Note. Total number of observations in the sample is 92.
| Revision | Advanced estimate | ||||
|---|---|---|---|---|---|
| Less than 0 | 0 to 2 | 2 to 4 | 4 to 6 | More than 6 | |
| Greater than 2 | 0 | 2 | 1 | 2 | 0 |
| 0 to 2 | 3 | 14 | 23 | 5 | 0 |
| –2 to 0 | 2 | 7 | 15 | 6 | 1 |
| –4 to –2 | 0 | 3 | 3 | 4 | 0 |
| Less than –4 | 1 | 0 | 0 | 0 | 0 |
Note. Total number of observations in the sample is 92.
In the 2013 comprehensive revision of the NIPAs, a new category of investment called intellectual property products (IPP) was added; this category consists of research and development, entertainment, literary, artistic originals, and software. This last component, software, was also measured before but was bundled with equipment in a category called equipment and software.
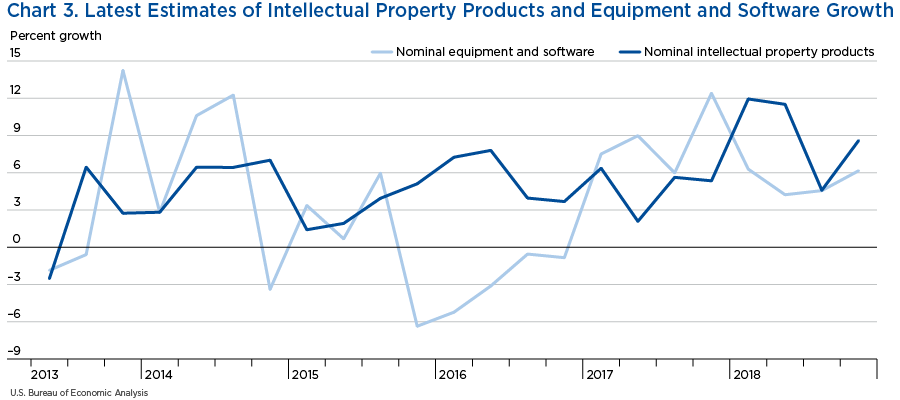
Charts 3 and 4 make the case for creating a new category on its own, instead of expanding equipment and software to equipment and IPP. For example, chart 3 compares the latest estimates of growth of nominal equipment and software and IPP since the series of IPP is publicly available, and by looking at the chart one can see that the growth rates of both types of investment are quite different both in their levels and in their cyclical properties.
This is not surprising since investment in equipment is usually expensive and lumpy, while investment in IPP is not, and the depreciation rates of both types of investment are also significantly different.4
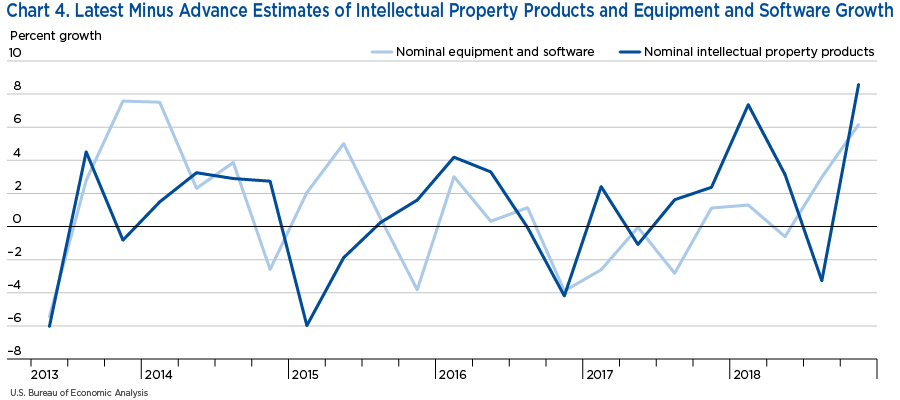
Moreover, chart 4 also shows that the quarterly revisions between the advance estimate of each series and its latest growth estimates, although similar in magnitude, are quite different through time and don't follow similar patterns.
Now we turn our focus on the properties of the IPP growth estimates that BEA has published since 2013.
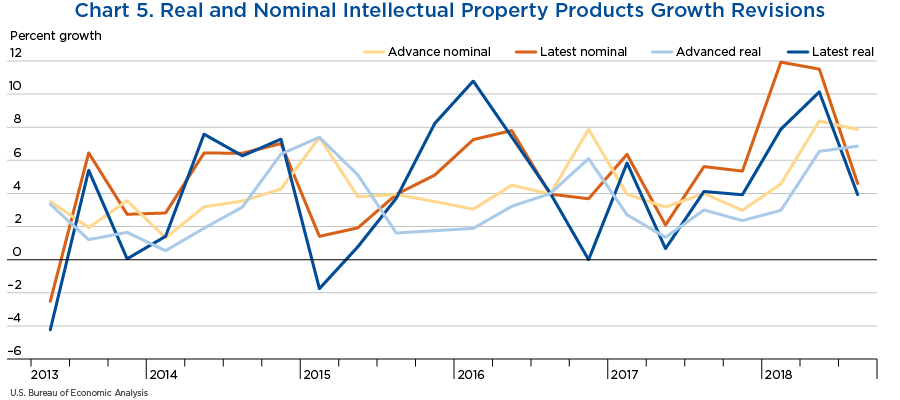
Charts 5 and 6 show the evolution of the real and nominal growth estimates of IPP, from the advance quarterly estimates to the latest ones available.
Chart 5 shows that even though the early estimates of real and nominal growth, as well as the latest estimates, are positively correlated, there is no systematic pattern between the advance and the latest series.5 Sometimes advance estimates of growth are above final estimates, but some other times they are below. And similarly, real and nominal growth estimates cross multiples times throughout the sample, showing no systematic pattern between the real and nominal series either.
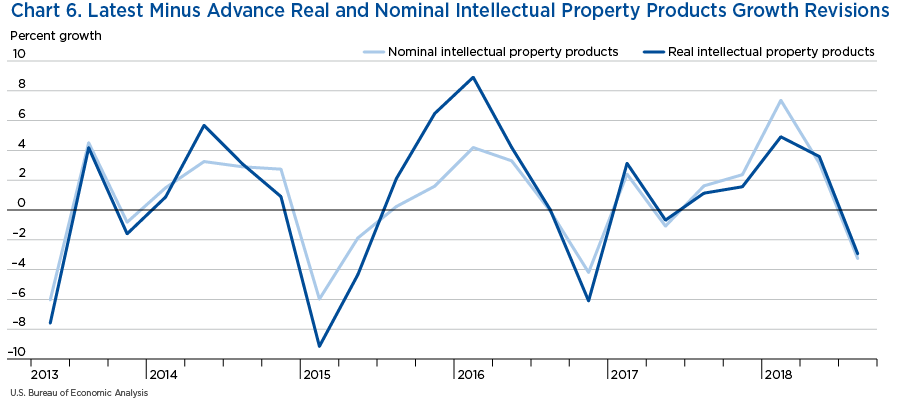
Lastly, chart 6 shows the differences between the latest and advance growth estimates for the real and nominal IPP quarterly growth. As one can see, the differences in the revisions from latest to advance are very similar for both the nominal and real estimates, (with maybe a noticeable gap between the two series at the end of 2015 and the beginning of 2016, when there was a strong real growth in IPP), with a much more modest growth in nominal terms, indicative of falling prices at least for some of the components inside the IPP category.
Table 7 presents the MRs and MARs of the revisions to quarterly estimates of GDI. Note that some categories of GDI are revised more than others, like national income and corporate profits, whose first estimates are released at the same time as the third revisions of the other components of GDI. Consequently, advance estimates of GDI are not prepared, and since 1995, second current quarterly estimates of GDI in the fourth quarter of each year have not been prepared either. The reason that these estimates of GDI are not produced is mainly because there is a lack of reliable source data for estimating corporate profits, which affects several other components of GDI. Advance and second estimates are prepared for the other major components of GDI, such as compensation of employees and proprietors' income.
Beginning with the first quarter of 2002, a fourth vintage of the estimates for the previous quarter has been prepared using data from the Bureau of Labor Statistics (BLS) QCEW. These data are used to revise the estimates of compensation of employees, national income, and GDI. The fourth vintage is released at the time of the second quarterly estimate of the following quarter. However, the fourth vintage MR and MAR numbers are not shown in table 7.
| Vintage | Mean absolute revision | Mean revision | Standard deviation |
|---|---|---|---|
| Gross domestic income | |||
| Third | 1.62 | 0.01 | 2.10 |
| First annual | 1.65 | 0.04 | 2.07 |
| Second annual | 1.18 | 0.15 | 1.64 |
| Third annual | 0.95 | 0.18 | 1.24 |
| Private consumption of fixed capital | |||
| Advance | 6.17 | 0.18 | 18.41 |
| Second | 6.09 | 0.14 | 18.42 |
| Third | 6.58 | −0.49 | 22.77 |
| First annual | 6.59 | −1.36 | 23.48 |
| Second annual | 6.05 | −1.35 | 23.60 |
| Third annual | 6.48 | −1.58 | 24.27 |
| Taxes on production and imports | |||
| Advance | 2.45 | 0.38 | 3.28 |
| Second | 2.49 | 0.46 | 3.36 |
| Third | 2.30 | 0.53 | 3.20 |
| First annual | 2.00 | 0.51 | 2.80 |
| Second annual | 1.76 | 0.32 | 2.65 |
| Third annual | 1.70 | 0.09 | 2.74 |
| National income | |||
| Third | 2.75 | −0.01 | 3.74 |
| First annual | 2.10 | 0.12 | 2.85 |
| Second annual | 1.75 | 0.14 | 2.61 |
| Third annual | 1.54 | 0.16 | 2.46 |
| Compensation of employees | |||
| Advance | 2.29 | 0.14 | 3.10 |
| Second | 2.32 | 0.04 | 3.11 |
| Third | 2.30 | 0.01 | 3.11 |
| First annual | 1.69 | 0.03 | 2.34 |
| Second annual | 1.30 | 0.06 | 1.79 |
| Third annual | 1.04 | 0.11 | 1.49 |
| Proprietors' income | |||
| Advance | 5.94 | 0.69 | 7.53 |
| Second | 6.00 | 0.62 | 7.63 |
| Third | 6.00 | 0.73 | 7.70 |
| First annual | 6.63 | 0.70 | 8.14 |
| Second annual | 5.39 | 0.87 | 6.81 |
| Third annual | 5.31 | 0.67 | 8.11 |
| Nonfarm proprietors' income | |||
| Advance | 5.61 | 0.55 | 7.37 |
| Second | 5.59 | 0.45 | 7.35 |
| Third | 5.58 | 0.51 | 7.37 |
| First annual | 5.87 | 0.94 | 7.39 |
| Second annual | 5.06 | 0.90 | 6.57 |
| Third annual | 5.03 | 0.65 | 8.18 |
| Corporate profits with inventory valuation adjustment and capital consumption adjustment | |||
| Third | 16.28 | −1.81 | 24.49 |
| First annual | 12.39 | −0.92 | 18.49 |
| Second annual | 9.00 | −0.85 | 16.31 |
| Third annual | 6.28 | −0.33 | 11.68 |
| Net interest and miscellaneous payments | |||
| Advance | 13.92 | 2.73 | 23.76 |
| Second | 16.45 | 2.72 | 21.38 |
| Third | 16.17 | 2.14 | 21.28 |
| First annual | 14.73 | 2.35 | 19.63 |
| Second annual | 12.06 | 1.72 | 15.74 |
| Third annual | 10.39 | −0.84 | 13.99 |
The MAR for the early annual estimates of GDI (to the latest estimate) is 1.62 percentage points. It increases with the first annual estimates and then declines with the second and third annual estimates. This is comparable to the MAR for real GDP (table 3), which shows an increase from the advance estimates to the third estimates before declining for the subsequent estimates. The MARs for most of the components of GDI tend to decline with successive vintages of estimates, with a few exceptions: private consumption of fixed capital, proprietors' income, and nonfarm proprietors' income. Another notable observation from table 7 is that the MARs for GDI components can be significantly larger than the MAR for total GDI. For example, the MARs for corporate profits is about 10 times larger than those for GDI, and the MARs for private consumption of fixed capital is about 5 times larger than those for GDI.
The MRs for GDI and its major components are much smaller than the corresponding MARs, and the MRs for any given component can have a mixture of positive and negative signs for different vintages. Private consumption of fixed capital and corporate profits have only negative MRs for all vintages; in contrast, taxes on production and imports, compensation of employees, proprietors' income, and nonfarm proprietors' income have only positive MRs for all vintages. Additionally, like the GDP shown in table 1, the MRs do not tend to decline with successive vintages of estimates.
Table 8 presents additional information on the standard deviation measures of GDI estimates. The scaled standard deviations provide a sense of how volatile the revisions can be, taking into account the variability of the estimates themselves. The scaled standard deviations for GDI are rather small, all less than 1 percentage point for all vintages. For all other components of GDI, the scaled standard deviations are similar to those of aggregate GDI. However, in stark contrast to all the other components, the scaled standard deviations of private consumption of fixed capital are above 6 percentage points for all vintages, and the standard deviations gets larger with each successive vintage.
| Vintage | Standard deviation of estimates | Standard deviation of revisions | Scaled standard deviation |
|---|---|---|---|
| Gross domestic income | 3.09 | ||
| Third | 2.10 | 0.68 | |
| First annual | 2.07 | 0.67 | |
| Second annual | 1.64 | 0.53 | |
| Third annual | 1.24 | 0.40 | |
| Private consumption of fixed capital | 2.57 | ||
| Advance | 18.41 | 7.15 | |
| Second | 18.42 | 7.16 | |
| Third | 22.77 | 8.85 | |
| First annual | 23.48 | 9.12 | |
| Second annual | 23.60 | 9.17 | |
| Third annual | 24.27 | 9.43 | |
| Taxes on production and imports | 3.30 | ||
| Advance | 3.28 | 0.99 | |
| Second | 3.36 | 1.02 | |
| Third | 3.20 | 0.97 | |
| First annual | 2.80 | 0.85 | |
| Second annual | 2.65 | 0.80 | |
| Third annual | 2.74 | 0.83 | |
| National income | 3.59 | ||
| Third | 3.74 | 1.04 | |
| First annual | 2.85 | 0.79 | |
| Second annual | 2.61 | 0.73 | |
| Third annual | 2.46 | 0.69 | |
| Compensation of employees | 3.69 | ||
| Advance | 3.10 | 0.84 | |
| Second | 3.11 | 0.84 | |
| Third | 3.11 | 0.84 | |
| First annual | 2.34 | 0.63 | |
| Second annual | 1.79 | 0.48 | |
| Third annual | 1.49 | 0.40 | |
| Proprietors' income | 7.92 | ||
| Advance | 7.53 | 0.95 | |
| Second | 7.63 | 0.96 | |
| Third | 7.70 | 0.97 | |
| First annual | 8.14 | 1.03 | |
| Second annual | 6.81 | 0.86 | |
| Third annual | 8.11 | 1.02 | |
| Nonfarm proprietors' income | 7.70 | ||
| Advance | 7.37 | 0.96 | |
| Second | 7.35 | 0.95 | |
| Third | 7.37 | 0.96 | |
| First annual | 7.39 | 0.96 | |
| Second annual | 6.57 | 0.85 | |
| Third annual | 8.18 | 1.06 | |
| Corporate profits with inventory valuation adjustment and capital consumption adjustment | 23.36 | ||
| Third | 24.49 | 1.05 | |
| First annual | 18.49 | 0.79 | |
| Second annual | 16.31 | 0.70 | |
| Third annual | 11.68 | 0.50 | |
| Net interest and miscellaneous payments | 17.41 | ||
| Advance | 23.76 | 1.36 | |
| Second | 21.38 | 1.23 | |
| Third | 21.28 | 1.22 | |
| First annual | 19.63 | 1.13 | |
| Second annual | 15.74 | 0.90 | |
| Third annual | 13.99 | 0.80 |
Table 9 presents the full MAR triangle for GDI and its major components. Note that a fourth vintage is presented for compensation, national income, and total GDI that incorporates data from the QCEW. However, the fourth statistics should be viewed with caution because no fourth estimates were prepared before the first quarter of 2002, and the statistics are not fully compatible with the rest of the entries, which are for 1996–2018. Thus, the MARs for the fourth estimates are not discussed.
| Vintage | Second | Third | Fourth1 | Annual | Latest | ||
|---|---|---|---|---|---|---|---|
| First | Second | Third | |||||
| Gross domestic income | |||||||
| Third | 1.20 | 1.17 | 1.28 | 1.55 | 1.62 | ||
| Fourth | 0.89 | 1.06 | 1.22 | 1.86 | |||
| First annual | 1.21 | 1.44 | 1.65 | ||||
| Second annual | 0.84 | 1.18 | |||||
| Third annual | 0.95 | ||||||
| Private consumption of fixed capital | |||||||
| Advance | 0.48 | 1.51 | … | 3.16 | 2.93 | 3.43 | 6.17 |
| Second | 1.15 | … | 3.09 | 2.90 | 3.39 | 6.09 | |
| Third | … | 2.62 | 2.40 | 2.85 | 6.58 | ||
| First annual | 1.91 | 2.41 | 6.59 | ||||
| Second annual | 1.13 | 6.05 | |||||
| Third annual | 6.48 | ||||||
| Taxes on production and imports | |||||||
| Advance | 0.64 | 1.39 | … | 1.66 | 1.71 | 1.89 | 2.45 |
| Second | 1.20 | … | 1.62 | 1.75 | 1.97 | 2.49 | |
| Third | … | 1.34 | 1.51 | 1.81 | 2.30 | ||
| First annual | 1.02 | 1.40 | 2.00 | ||||
| Second annual | 0.98 | 1.76 | |||||
| Third annual | 1.70 | ||||||
| National income | |||||||
| Third | 2.36 | 2.02 | 2.04 | 2.13 | 2.75 | ||
| Fourth | 1.12 | 1.44 | 1.70 | 2.66 | |||
| First annual | 1.33 | 1.75 | 2.10 | ||||
| Second annual | 1.12 | 1.75 | |||||
| Third annual | 1.54 | ||||||
| Compensation of employees | |||||||
| Advance | 0.48 | 0.60 | 2.22 | 1.93 | 2.05 | 2.29 | 2.29 |
| Second | 0.16 | 2.16 | 1.89 | 2.02 | 2.24 | 2.32 | |
| Third | 2.13 | 1.87 | 2.01 | 2.22 | 2.30 | ||
| Fourth | 0.77 | 1.01 | 1.03 | 1.75 | |||
| First annual | 1.20 | 1.39 | 1.69 | ||||
| Second annual | 0.71 | 1.30 | |||||
| Third annual | 1.04 | ||||||
| Proprietors' income | |||||||
| Advance | 0.99 | 1.34 | … | 3.60 | 4.67 | 5.20 | 5.94 |
| Second | 0.79 | … | 3.68 | 4.65 | 5.27 | 6.00 | |
| Third | … | 3.50 | 4.61 | 5.35 | 6.00 | ||
| First annual | 4.30 | 5.83 | 6.63 | ||||
| Second annual | 3.60 | 5.39 | |||||
| Third annual | 5.31 | ||||||
| Nonfarm proprietors' income | |||||||
| Advance | 0.65 | 0.86 | … | 2.54 | 3.95 | 4.84 | 5.61 |
| Second | 0.51 | … | 2.48 | 3.93 | 4.79 | 5.59 | |
| Third | … | 2.58 | 3.95 | 4.78 | 5.58 | ||
| First annual | 3.30 | 5.45 | 5.87 | ||||
| Second annual | 3.86 | 5.06 | |||||
| Third annual | 5.03 | ||||||
| Corporate profits with inventory valuation adjustment and capital consumption adjustment | |||||||
| Third | … | 8.00 | 12.12 | 14.30 | 16.28 | ||
| First annual | 7.30 | 10.85 | 12.39 | ||||
| Second annual | 7.41 | 9.00 | |||||
| Third annual | 6.28 | ||||||
| Net interest and miscellaneous payments | |||||||
| Advance | 1.67 | 3.26 | … | 6.62 | 8.44 | 10.69 | 13.92 |
| Second | 3.32 | … | 7.82 | 10.81 | 12.96 | 16.45 | |
| Third | … | 7.76 | 10.82 | 13.06 | 16.17 | ||
| First annual | 9.11 | 12.18 | 14.73 | ||||
| Second annual | 7.69 | 12.06 | |||||
| Third annual | 10.39 | ||||||
- Fourth estimates began in 2002, and apply only to GDI, national income, and compensation of employees.
The patterns of MARs for successive vintages of estimates and vintages of standards in table 9 for GDI are, for the most part, similar to those for GDP. For example, the MARs for GDI from the third estimates to the third annual estimates decline overall, but the MAR of the first annual estimate doesn't follow this pattern. The increases in MARs for the various vintages of GDI estimates are not monotonic when later vintages of estimates are used as standards. Lastly, the whole set of MARs for GDI tends to be modestly larger than the comparable ones for GDP.
Of all the components of GDI, the MARs reported for compensation of employees appear to be the smallest, with noticeably sharp drops in MARs moving from the third estimate to the fourth estimate, regardless of which vintage is used as the standard. MARs for national income are similar to those of compensation of employees; they also show that sharp drops in MARs occur from the third estimate to the fourth estimate, again regardless of which vintage is used as the standard. Even though the MARs for national income and compensation of employees are relatively small compared to the other GDI components, they are still larger than the MARs reported for aggregate GDI.
The patterns for GDI and its components are generally similar to the patterns for current-dollar GDP, but there are deviations; that is, the MARs for GDI and its components sometimes decrease from vintage to vintage used as the standards (rows) or increase from vintage to vintage of the estimates for any given standard (columns). Nevertheless, there is a tendency toward increases across rows of table 9 and decreases down the columns. In general, the MARs for the various components and vintages tend to be larger than those for the various GDP components.
Table 10 and table 11 present supplemental information about the revisions for GDI. Table 10 focuses on the third to latest estimate of GDI and its major components and provides additional information about the distribution of the revisions. The revisions appear to hover around the mean and the proportion of revisions within one standard deviation from the mean approximate to what one would observe for normally distributed random variables.
| Component | Minus 1 standard deviation | Mean | Plus 1 standard deviation | Number of observations within 1 standard deviation | Percentage of observations within 1 standard deviation |
|---|---|---|---|---|---|
| Gross domestic income | −2.08 | 0.01 | 2.10 | 65 | 71 |
| Private consumption of fixed capital | −23.13 | −0.49 | 22.16 | 88 | 96 |
| Taxes on production and imports | −2.67 | 0.52 | 3.71 | 72 | 78 |
| National income | −3.76 | −0.03 | 3.69 | 70 | 76 |
| Compensation of employees | −3.10 | 0.01 | 3.12 | 68 | 74 |
| Proprietors' income | −6.97 | 0.73 | 8.44 | 65 | 71 |
| Nonfarm proprietors' income | −6.83 | 0.50 | 7.82 | 69 | 75 |
| Corporate profits with inventory valuation adjustment and capital consumption adjustment | −26.14 | −1.79 | 22.57 | 74 | 80 |
| Net interest and miscellaneous payments | −19.18 | 2.02 | 23.23 | 66 | 72 |
Note. Total number of observations in the sample is 92.
| Revision | Advanced estimate | |||||
|---|---|---|---|---|---|---|
| Less than 0 | 0 to 2 | 2 to 4 | 4 to 6 | 6 to 8 | More than 6 | |
| Greater than 4 | 1 | 0 | 2 | 1 | 0 | 0 |
| 2 to 4 | 1 | 0 | 4 | 3 | 3 | 1 |
| 0 to 2 | 0 | 2 | 8 | 11 | 5 | 1 |
| −2 to 0 | 1 | 3 | 13 | 7 | 8 | 4 |
| −4 to −2 | 0 | 0 | 3 | 2 | 5 | 0 |
| Less than −4 | 1 | 0 | 0 | 1 | 0 | 0 |
Note. Total number of observations is 91.
In the United States, the National Bureau of Economic Research (NBER) Business Cycle Dating Committee maintains a chronology of U.S. business cycles. NBER emphasizes that a recession involves a significant decline in economic activity that is spread across the economy and lasts more than a few months. In practical terms, NBER uses three criteria—depth, diffusion, and duration—to determine the onset, length, and end of a recession, and these criteria are at least somewhat interchangeable.
In choosing the dates of business cycle turning points, NBER follows real GDP as the single best measure of aggregate economic activity, paying close attention to the two ways BEA measures this concept, from the product side (real GDP) and from the income side (real GDI). Additionally, NBER also considers total payroll employment as measured by BLS as well as other timelier economic indicators.
Lastly, and to avoid the need for major revisions, NBER waits to determine the date of a peak in activity, and thus the onset of recession, until confident that, even in the event that activity began to rise again immediately, a recession has occurred. Although this delay is understandable, a timely public policy and decision making are key to mitigate the effects of recessions, and that is why there are numerous models in different public institutions estimating the probability of being in a recession.6
Analogously, the same process takes place determining the end of a recession, so effectively there is a delay of a number of months identifying the peaks and troughs of recessions.
Our sample period from 1996 to 2018 covers two of the last recessions registered by NBER, the first one started in March 2001 (first quarter), and finished in November of the same year (fourth quarter), and the second one was the Great Recession, that officially started in December 2007 (fourth quarter) and ended in June 2009 (second quarter).
Galvão and Kara (2020) find that data revisions to U.K. GDP lead to a turning point chronology that has fewer and shorter recessions than real-time chronologies that rely on early estimates of GDP.
As mentioned before, in the United States, NBER determines the length of recessions with a very significant delay, as seen in table 12, so the chronology of recessions is never revised, but we can see ex-post how our knowledge of a recession changed with time and data.
For example, by comparing the early and the latest vintages of quarterly growth produced by BEA as they were being released during recessions, we can explore whether the growth rates from beginning to end of a recession vary by vintages and how our knowledge of a recession was changing at the time of the recession. Of special interest would be to see if in line with the U.K. findings of shorter recessions, we find that recessions in the United States also turn out to be shorter or milder when we use more recent vintages containing more data and information.
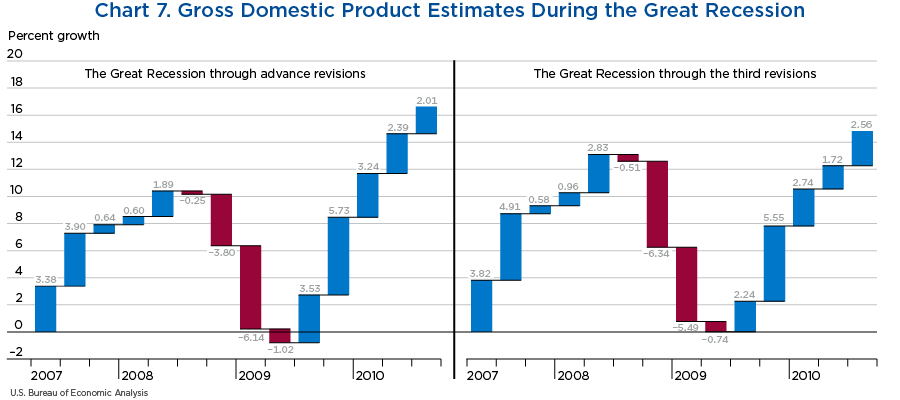
BEA publishes early estimates of quarterly GDP growth the month after the quarter has passed so early estimates of a first, second, third, and fourth quarter are published in April, July, and October of a given year, and January of the following year. These are the estimates in the left panel of chart 7.
The second estimates come a month after the early estimates, and the third ones, a month after the second ones, so for example, by the time the early estimate of third quarter is released in October, the third estimate of the second quarter is already available (as it was released in September), and so on.
Other papers, like Jordà et al. (2020) try to predict the size of the GDP growth revisions from the advance to the second and third revisions, using complementary economic indicators and economic theory, to improve economic policy making in real time, especially during recessions.
Although their approach is very valuable, in this paper we take a different turn and focus exclusively on BEA-released data to analyze when we knew what in times of economic turbulence.
Thus, the right panel of chart 8 shows the third estimates during the Great Recession.
The differences between the two panels in chart 7 are visible, but small, in the sense that they didn't significantly change our picture of what was happening at the time. For example, by looking at the third revisions, the peak or turning point from the previous expansion didn't change from the early to the third revision and continued to be the fourth quarter of 2007, although the growth rates leading to this quarter had been stronger than we originally thought. Similarly, the growth in the second quarter of 2008 was stronger than anticipated, but the last quarter of 2008 and first quarter of 2009 were both very negative and similar in magnitude; although the first quarter of 2009 was slightly less negative than the last quarter of 2008, it was too close to affirm that the worst had passed already and we had begun to turn a corner.
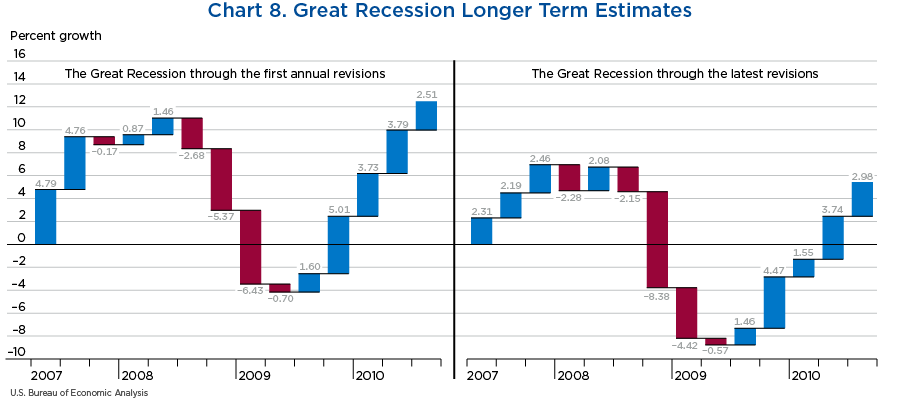
BEA also conducts annual revisions (three in total) of quarterly growth every July; that is, the first annual revisions of all quarter growth estimates in a year are released in July of the following year. Moreover, the first major revision of a first-quarter growth estimate in a year is also released in July of that same year, together with the first annual revisions from the previous year's quarters mentioned above.
In chart 8 below, the left panel shows the first major revision of the first quarters and the first annual revisions of the second, third, and fourth quarters around the Great Recession. The panel on the right shows the latest growth estimates available, which include not only all the data available many years later, but also comprehensive revisions to how we measure GDP.
The first major annual revisions of the last quarter of 2008 and the first quarter of 2009 shown in the left panel were released at the end of July 2009, timidly reversing the idea that the worst had happened in the last quarter of 2008, and instead hinting that the economy had continued worsening during the first quarter of 2009. The first annual revision also highlighted for the first time that economic activity during the third quarter of 2008 had contracted significantly.
Subsequent annual revisions of the quarters around the Great Recession didn't change the picture on the left panel of chart 8, so with this and other economic data, NBER dated the peak and trough around the Great Recession as December 2007, at the end of the fourth quarter of that year, and June 2009, at the end of the second quarter. However, after the later comprehensive revisions shown in the right panel of chart 8, the length of the Great Recession was shorter than what earlier estimates signaled, in line with what Galvão and Kara (2020) found for the United Kingdom, but also deeper than what we previously believed.
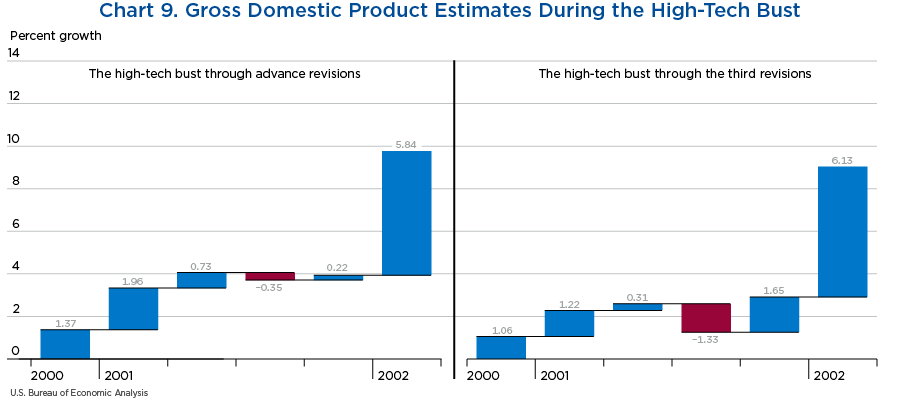
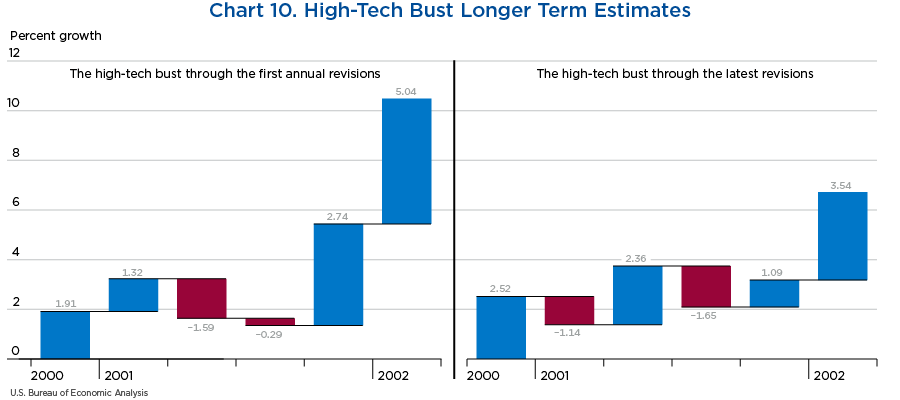
Next, we conduct a similar graphical analysis of the data released during and after the “high tech” bust of 2001 in charts 9 and 10, showing data from 2000 Q4 to 2002 Q1. The peak and trough of this recession seems to have changed when comparing the four panels of these charts, with only the latest estimates of quarterly growth shown in the right panel of chart 10 coinciding with the turning points dates announced by NBER and shown in table 12.
| Turning point date | Peak or trough | Announcement date |
|---|---|---|
| December 2007 | Peak | December 2008 |
| June 2009 | Trough | September 2010 |
| March 2001 | Peak | November 2001 |
| November 2001 | Trough | July 2003 |
Source: National Bureau of Economic Research.
However, when looking at the depth of the recession with the luxury of time, the latest estimates of the high tech bust show a deeper fall in economic activity than what we believed was going on at the time of the recession, just as charts 7 and 8 showed for the Great Recession.
Table 13 shows summary statistics for revisions of the different annual estimates to the latest estimates for both real and current-dollar GDP and their major components. Like the quarterly estimates, the MRs for the annual estimates are small in magnitude and vary in direction. The early annual estimates are those that become available in March of the following year and are mostly composed of third current quarterly estimates, excluding the fourth-quarter numbers, and thus their MRs are similar to those of previous quarterly estimates.
| Vintage | Mean revision | Mean absolute revision | ||
|---|---|---|---|---|
| Current-dollar | Real | Current-dollar | Real | |
| Gross domestic product | ||||
| Early annual | 0.03 | −0.05 | 0.42 | 0.41 |
| First annual | −0.01 | 0.03 | 0.31 | 0.34 |
| Second annual | 0.10 | 0.16 | 0.25 | 0.27 |
| Third annual | 0.11 | 0.17 | 0.20 | 0.21 |
| Personal consumption expenditures | ||||
| Early annual | −0.05 | −0.05 | 0.38 | 0.35 |
| First annual | −0.15 | −0.06 | 0.34 | 0.33 |
| Second annual | −0.03 | 0.06 | 0.28 | 0.29 |
| Third annual | 0.08 | 0.14 | 0.23 | 0.24 |
| Gross private domestic investment | ||||
| Early annual | 0.25 | 0.13 | 1.39 | 1.63 |
| First annual | 0.48 | 0.42 | 1.39 | 1.35 |
| Second annual | 0.77 | 0.83 | 1.19 | 1.29 |
| Third annual | 0.64 | 0.66 | 1.08 | 1.11 |
| Fixed investment | ||||
| Early annual | 0.25 | 0.15 | 0.91 | 1.07 |
| First annual | 0.30 | 0.30 | 0.96 | 0.98 |
| Second annual | 0.71 | 0.77 | 0.96 | 1.07 |
| Third annual | 0.47 | 0.69 | 0.80 | 1.03 |
| Change in private inventories1 | ||||
| Net exports of goods and services1 | ||||
| Exports | ||||
| Early annual | 0.06 | 0.23 | 0.67 | 0.66 |
| First annual | 0.27 | 0.37 | 0.51 | 0.63 |
| Second annual | 0.06 | 0.16 | 0.38 | 0.49 |
| Third annual | 0.03 | 0.14 | 0.31 | 0.38 |
| Imports | ||||
| Early annual | 0.18 | 0.52 | 0.51 | 0.70 |
| First annual | 0.19 | 0.40 | 0.26 | 0.54 |
| Second annual | 0.08 | 0.29 | 0.21 | 0.45 |
| Third annual | 0.07 | 0.21 | 0.16 | 0.33 |
| Federal government | ||||
| Early annual | −0.01 | −0.11 | 0.51 | 0.56 |
| First annual | −0.29 | −0.15 | 0.51 | 0.43 |
| Second annual | −0.30 | −0.14 | 0.37 | 0.31 |
| Third annual | −0.33 | −0.04 | 0.43 | 0.31 |
| State and local government | ||||
| Early annual | 0.36 | −0.04 | 1.05 | 0.90 |
| First annual | 0.26 | 0.09 | 0.79 | 0.79 |
| Second annual | 0.22 | 0.08 | 0.77 | 0.64 |
| Third annual | 0.05 | 0.00 | 0.57 | 0.23 |
- Percent changes cannot be calculated because of the presence of both positive and negative values.
The MARs are considerably smaller than the current quarterly estimates for both real and current-dollar GDP. One important reason is that annual frequency estimates are not subject to revisions to seasonal adjustment factors, and the other, of course, is that they aggregate activity during a longer period of time where misses in one quarter are going to be captured in another quarter, or simply compensated for by opposite misses in another. The MARs show a tendency to decline over each vintage both in current-dollar and real-dollar estimates. Moreover, MARs also decline steadily across vintages for the underlying components. As with total GDP, the MARs of components are much smaller than those for quarterly estimates.
Revisions in definitions, as part of comprehensive NIPA revisions, have generally resulted in increases to the growth rates of GDP. For example, the introduction of software as investment in the 1999 comprehensive revision raised both the levels and the growth rates of GDP. However, the introduction of research and development (R&D) and artistic originals as investment in the 2013 comprehensive revision raised the levels of GDP but did little to change the growth rates. The reason is that once R&D and artistic originals were included in the early estimates of 2013 in the new investment category of IPP, together with software, posterior revisions of this investment were incorporated into the years prior to 2013, in order to acknowledge that these products existed before and had been growing in importance before they were introduced in the national accounts. See the section on IPP above where we discuss in detail the introduction of the IPP category, separate from investment in equipment. Lastly, for a broader discussion about the effects of comprehensive revisions on the estimates, see Fixler, Greenaway-McGreevey, and Grimm (2014).
Table 14 presents summary statistics for revisions of annual estimates of GDI growth rates and its major components. The estimates are expressed in terms of percentage points of the annual estimates. As with the quarterly estimates, the MRs are small in magnitude and vary in sign. The early annual estimates are similar to the third current quarterly estimates, and their MRs are therefore similar to those of previous estimates of the same vintage.
| Vintage | Mean revision | Mean absolute revision |
|---|---|---|
| Gross domestic income | ||
| Early annual | 0.12 | 0.67 |
| First annual | 0.10 | 0.52 |
| Second annual | 0.11 | 0.29 |
| Third annual | 0.20 | 0.36 |
| Private consumption of fixed capital | ||
| Early annual | 0.76 | 1.56 |
| First annual | 0.34 | 1.22 |
| Second annual | 0.50 | 1.18 |
| Third annual | −0.05 | 0.86 |
| Taxes on production and imports | ||
| Early annual | 0.60 | 1.07 |
| First annual | 0.41 | 0.74 |
| Second annual | 0.27 | 0.53 |
| Third annual | 0.16 | 0.46 |
| National income | ||
| Early annual | −3.33 | 3.87 |
| First annual | 0.16 | 0.62 |
| Second annual | 0.13 | 0.44 |
| Third annual | 0.21 | 0.42 |
| Compensation of employees | ||
| Early annual | 0.03 | 0.72 |
| First annual | 0.09 | 0.25 |
| Second annual | 0.13 | 0.31 |
| Third annual | 0.05 | 0.30 |
| Proprietors' income | ||
| Early annual | 0.77 | 3.90 |
| First annual | 0.87 | 4.17 |
| Second annual | 0.90 | 3.11 |
| Third annual | 0.95 | 2.62 |
| Nonfarm proprietors' income | ||
| Early annual | 0.78 | 4.18 |
| First annual | 0.87 | 4.25 |
| Second annual | 0.92 | 3.17 |
| Third annual | 1.23 | 2.88 |
| Rental income of persons | ||
| Corporate profits with inventory valuation adjustment and capital consumption adjustment | ||
| Early annual | −1.22 | 5.71 |
| First annual | −0.79 | 4.10 |
| Second annual | −1.10 | 2.34 |
| Third annual | 0.15 | 1.98 |
| Net interest and miscellaneous payments | ||
| Early annual | 2.38 | 10.27 |
| First annual | 1.99 | 9.03 |
| Second annual | 1.27 | 4.87 |
| Third annual | −0.91 | 3.92 |
The MRs for GDI and its components are a fraction of the size of those for the current quarterly estimates. The same pattern is observed when comparing annual estimates of GDP with the quarterly estimates, and the same reasoning applies: annual estimates are not subject to revisions based on changes to seasonal adjustment factors. The MARs for GDI tend to decline with each successive estimate. These declines reflect the incorporation of newly received annual source data that is more complete or revised from earlier data. In particular, the second annual vintage is the first to incorporate data from the Statistics of Income database from the Internal Revenue Service (IRS), so the drop in MARs should be most noticeable moving from the first annual estimate to the second annual estimate for GDI and its components. For example, the MAR for GDI declines 0.23 percentage point from the first annual estimate to second annual estimate and then increases slightly to the third annual estimate. The MAR for net interest is notable, dropping 4.16 percentage points from the first annual estimate to the second annual estimate.
In national economic accounting, GDP and GDI are conceptually equal, but practically different. GDP measures overall economic activity by final expenditures, and GDI measures economic activity by the incomes generated from producing the goods and services inside GDP. In practice, GDP and GDI differ because they are constructed using different sources of information, both imperfect in different ways. The different source data produce different results for a number of reasons, including sampling errors, coverage differences, and timing differences with respect to when expenditures and incomes are recorded.7
Charts 11 and 12 show that for most of our sample, estimates of real GDP and GDI growth give a similar picture of the economy.
In the end, GDP and GDI are two ways of measuring aggregate economic activity, so while some of BEA's data users prefer one over the other, many users like to have both sets of information since they complement each other. Thus, in response to this demand from its data users, in July 2015 BEA started publishing a new series that averages GDP and GDI, providing users another way to track U.S. economic growth.
| Mean absolute revisions | ||||
|---|---|---|---|---|
| Vintage | Vintage of revision used as standard | |||
| First annual | Second annual | Third annual | Latest | |
| Average of gross domestic product (GDP) and gross domestic income (GDI) | ||||
| Third | 0.74 | 0.95 | 1.12 | 1.21 |
| First annual | 0.73 | 0.94 | 1.03 | |
| Second annual | 0.58 | 0.81 | ||
| Third annual | 0.65 | |||
| GDP alone | ||||
| Third | 0.77 | 0.98 | 1.14 | 1.35 |
| First annual | 0.64 | 0.80 | 1.02 | |
| Second annual | 0.48 | 0.87 | ||
| Third annual | 0.69 | |||
| GDI alone | ||||
| Third | 0.97 | 1.26 | 1.63 | 1.68 |
| First annual | 1.12 | 1.49 | 1.63 | |
| Second annual | 0.93 | 1.13 | ||
| Third annual | 0.94 | |||
| Mean revisions | ||||
| Vintage | Vintage of revision used as standard | |||
| First annual | Second annual | Third annual | Latest | |
| Average of gross domestic product (GDP) and gross domestic income (GDI) | ||||
| Third | −0.04 | −0.14 | −0.22 | −0.02 |
| First annual | −0.10 | −0.18 | 0.02 | |
| Second annual | −0.07 | 0.12 | ||
| Third annual | 0.17 | |||
| GDP alone | ||||
| Third | 0.01 | −0.13 | −0.12 | −0.03 |
| First annual | −0.14 | −0.14 | −0.04 | |
| Second annual | 0.00 | 0.10 | ||
| Third annual | 0.10 | |||
| GDI alone | ||||
| Third | −0.09 | −0.16 | −0.31 | −0.01 |
| First annual | −0.07 | −0.22 | 0.08 | |
| Second annual | −0.15 | 0.15 | ||
| Third annual | 0.24 | |||
Note. Sample size is smaller for latest minus third annual since third annual estimates were not available beyond 2015:IV.
Table 15 presents the MARs and MRs of the current-dollar average of GDP and GDI series from the third estimate onwards compared with subsequent annual revisions and the latest available data.8 Because of the delay in the release of GDI estimates compared to GDP estimates, and in order to conduct a fair comparison across the vintages, the sample period used in the table runs from 1996 to 2018.9
The top half of the table reports the MARs of the average series and the stand-alone ones, and as expected, the numbers increase as later and later vintages are used as the standard. The MAR (and the corresponding MR) appear to be smallest going from the second annual estimate to the third annual estimate because by the second annual estimate, most of the information has been incorporated into the estimates already, and there are very little trend-based estimates and very little use of indirect sources. Moreover, most direct indicators have also been replaced by comprehensive data, so the change in data moving from the second annual revision to the third annual revision is minimal and involves only some additional conversion of direct indicators to comprehensive data.
The data shows that the MARs of the average series are smaller than the MARs for GDI for all vintages and smaller or equal to most of the MARs for GDP. If both GDP and GDI are interpreted as the sums of the unobserved true economic activity and of measurement errors, it is possible to infer that the weighted average series of the two is a more reliable measure of activity than either GDP or GDI alone. This occurs, of course, because some of the measurement errors are averaged out, reducing subsequent revisions in the weighted average. However, the better reliability observed using the average of GDP and GDI will not lead to a better understanding of the detailed workings of the economy because there is no obvious way of distributing the results of the averaging among the major components of GDP and GDI. Thus, the average series can only provide supplemental summary information about the recent course of the aggregate economy.
The bottom half of the table reports the MRs of the series of interest, and as one can see that for the third revision, MRs increase when the first annual estimate up to the third annual estimate are used as standards, but for the latest available estimate, the MR declines. Specifically, the MR for the average of GDP and GDI is −0.04 percentage point for the third vintage when the first annual revision is used as standard, and it increases to −0.14 percentage point when the second annual revision is used as standard instead, and increases a bit more when the third annual revision is standard. The MR then falls to −0.02 percentage point when comparing the latest estimate to the third annual estimate.
For the second annual vintage, the MR increases when the latest estimate is used as the standard rather than the third annual (from −0.07 percentage point to 0.12 percentage point). The same patterns are observed if we look at current-dollar GDP and GDI series on their own (just reported below in table 15 as well). The pattern may be explained by the fact that on average, for both GDP and GDI (and therefore, the average of GDP and GDI), the revisions are negative as later vintages are used as the standard except when moving from the third annual estimate to the latest available estimate. The explanation for this is that the revision produced by the latest available estimate less the third annual estimate includes comprehensive revisions, and on average this tends to be a relatively large positive number, thus reversing some of the negative revisions observed for earlier vintage comparisons.
BEA seeks to provide a timely, comprehensive, and accurate picture of the U.S. economy. However, because of the flow of source data over time, BEA provides vintages of estimates. This study examines how those vintage estimates vary. Throughout this study, we have shown that the different estimates of GDP and GDI that BEA publishes are reliable and that the differences in vintages estimates arise mostly by new information and not by measurement errors. More specifically, we have shown that that the estimates of GDP and GDI have small MARs and MRs for most quarters in our sample, consistent with previous similar BEA studies.
The average of GDP and GDI series appears to be a more reliable measure of aggregate economic activity than GDP and GDI taken separately in the sense that the MARs of the average series are smaller or equal compared to those of GDP and GDI taken individually. Moreover, when we take the MRs from the latest to the third estimates for GDP and GDI individually and compare the sign of these revisions side by side in every quarter in our sample, we find that in more than a third of cases, the latest revisions of GDP and GDI moved in opposite directions, that is, by looking at the third revisions, we were underestimating GDP and overestimating GDI or overestimating GDP and underestimating GDI. In these cases, combining these estimates is particularly useful to give us a more accurate picture of the economy, and it clearly shows that the data sources we use to compute these two estimates are different and convey information that is not always captured “properly” or in a timely manner in the other estimate, indicating that the estimates of GDP and GDI are complements.
However, the average series can only be constructed in the aggregate and with a delay because the results of the average cannot be distributed among the major components of GDP and GDI. A by-product of our analysis is a demonstration of the uncertainty surrounding the BEA estimates. We have shown that revision magnitudes can be used to construct confidence intervals. We have also shown that uncertainty surrounding estimates of turning points does not impact the qualitative nature of the analysis.
- For example, the accounts contain no entries for business investment in computer software before 1959; the amount of software prior to that year was negligible. But by 2012, business investment in software was 1.7 percent of the size of GDP; the level and rates of growth of the economy were raised when software investment was first included in the accounts in the late 1990s.
- The time period for this study is 1996–2018. A study of the most immediate revisions by Fixler, Kanal, and Tien (2018) covered data from 1993–2015. The years 1993–1996 from the last study do not exhibit any trends that affect the current study, so the sample years have been rolled over 3 years toward the present to make comparisons consistent with previous studies.
- Given a normal distribution, the standard deviation is a component of the statistic that tests the hypotheses that the MR is significantly different from zero.
- See comprehensive estimates of depreciation rates by type of assets in the paper “BEA Depreciation Rates.”
- The correlation between real and nominal IPP makes sense because nominal growth includes real growth (quantity) and price growth.
- See, for example, Pike and Vazquez-Grande (2019) or Ergungor (2016).
- For a detailed discussion of the timing of GDP and GDI estimates and the source data available for each estimate, see Fixler, Greenaway-McGreevey, and Grimm (2014) and Holdren (2014).
- GDI is not available when the advance estimates of GDP are released, and it is only available for the first three quarters of the year when it is released with the second estimate of GDP. Therefore, for a comparable and continuous quarterly average series, the third estimate would be the earliest vintage.
Ergungor, O.E. 2016. “Recession Probabilities,” Federal Reserve Bank of Cleveland, Economic Commentary 2016–09 (August).
Fixler, D.J., D. Kanal, and P-L.Tien, “The Revisions to GDP, GDI, and Their Major Components,” Survey of Current Business 98 (January 2018).
Fixler, D.J., R. Greenaway-McGreevey, and B.T. Grimm, “The Revisions to GDP, GDI, and Their Major Components,” Survey of Current Business 94 (August 2014).
Fixler, D.J., R. Greenaway-McGreevey, and B.T. Grimm, “The Revisions to GDP, GDI, and Their Major Components,” Survey of Current Business 91 (July 2011).
Galvão, A.B., and A. Kara. 2020. “The impact of GDP data revisions on identifying and predicting UK Recessions,” UK National Institute of Economic and Social Research, Economics Statistics Centre of Excellence Discussion Paper 2020–12 (July).
Holdren, A.E., “Gross Domestic Product and Gross Domestic Income: Revisions and Source Data,” Survey of Current Business 94 (June 2014).
Jordà, O., N. Kouchekinia, C. Merrill, and T. Sekhposyan. 2020. “The Fog of Numbers,” Federal Reserve Bank of San Francisco Economic Letter 2020–20 (July).
Kelly, P.A, S.H. McCulla, and D.B. Wasshausen, “Improved Estimates of the National Income and Product Accounts: Results of the 2018 Comprehensive Update,” Survey of Current Business 98 (September 2018).
Kuznets, S. 1948. “National Income: A New Version,” Review of Economics and Statistics 30 (August): 151–179.
Manski, C. F. 2015. “Communicating Uncertainty in Official Economic Statistics: An Appraisal Fifty Years after Morgenstern,” Journal of Economic Literature 53 (September): 631–653.
Pike, T. and F. Vazquez-Grande. 2019. “Out-of-Sample Performance of Recession Probability Models,” FEDS Notes 2019-12-13-1, Board of Governors of the U.S. Federal Reserve System.
| Vintage | Vintage of revision used as standard | |||||
|---|---|---|---|---|---|---|
| Second | Third | Annual | Latest | |||
| First | Second | Third | ||||
| Gross domestic product | ||||||
| Advance | 0.63 | 0.80 | 1.15 | 1.29 | 3.40 | 1.59 |
| Second | 0.36 | 0.98 | 1.20 | 3.46 | 1.53 | |
| Third | 0.98 | 1.18 | 3.40 | 1.51 | ||
| First annual | 0.79 | 3.04 | 1.27 | |||
| Second annual | 2.80 | 1.11 | ||||
| Third annual | 0.77 | |||||
| Personal consumption expenditures | ||||||
| Advance | 0.36 | 0.51 | 1.00 | 1.07 | 3.24 | 1.22 |
| Second | 0.38 | 0.85 | 0.95 | 3.21 | 1.12 | |
| Third | 0.81 | 0.92 | 3.17 | 1.07 | ||
| First annual | 0.69 | 3.08 | 0.92 | |||
| Second annual | 2.89 | 0.69 | ||||
| Third annual | 0.61 | |||||
| Gross private domestic investment | ||||||
| Advance | 3.32 | 3.54 | 6.20 | 6.50 | 8.43 | 6.35 |
| Second | 1.33 | 5.90 | 5.96 | 8.30 | 6.56 | |
| Third | 5.55 | 5.57 | 7.91 | 6.26 | ||
| First annual | 3.96 | 6.50 | 5.84 | |||
| Second annual | 4.93 | 4.47 | ||||
| Third annual | 3.58 | |||||
| Fixed investment | ||||||
| Advance | 1.33 | 1.61 | 2.94 | 3.40 | 5.53 | 3.51 |
| Second | 0.82 | 2.67 | 3.10 | 5.32 | 3.31 | |
| Third | 2.44 | 2.93 | 5.12 | 3.17 | ||
| First annual | 2.12 | 4.34 | 2.96 | |||
| Second annual | 3.60 | 2.05 | ||||
| Third annual | 2.13 | |||||
| Exports | ||||||
| Advance | 2.14 | 2.46 | 3.51 | 4.02 | 7.32 | 4.20 |
| Second | 1.27 | 2.70 | 3.26 | 7.07 | 3.57 | |
| Third | 2.60 | 3.05 | 6.84 | 3.39 | ||
| First annual | 2.17 | 6.44 | 2.84 | |||
| Second annual | 6.00 | 1.97 | ||||
| Third annual | 1.53 | |||||
| Imports | ||||||
| Advance | 2.37 | 2.73 | 3.93 | 4.30 | 10.81 | 4.40 |
| Second | 1.30 | 3.31 | 3.66 | 10.15 | 3.66 | |
| Third | 3.14 | 3.56 | 9.91 | 3.57 | ||
| First annual | 2.55 | 9.85 | 2.98 | |||
| Second annual | 9.54 | 2.43 | ||||
| Third annual | 2.14 | |||||
| Federal government | ||||||
| Advance | 0.95 | 0.92 | 2.56 | 2.76 | 4.87 | 4.01 |
| Second | 0.44 | 2.37 | 2.63 | 4.79 | 4.01 | |
| Third | 2.40 | 2.63 | 4.84 | 4.00 | ||
| First annual | 1.99 | 4.11 | 3.74 | |||
| Second annual | 3.64 | 3.47 | ||||
| Third annual | 3.48 | |||||
| State and local government | ||||||
| Advance | 0.88 | 0.98 | 3.34 | 1.72 | 4.57 | 2.00 |
| Second | 0.43 | 3.18 | 1.58 | 4.54 | 1.94 | |
| Third | 3.11 | 1.45 | 4.43 | 1.86 | ||
| First annual | 3.05 | 4.94 | 3.36 | |||
| Second annual | 3.98 | 1.40 | ||||
| Third annual | 1.32 | |||||
| Vintage | Vintage of revision used as standard | |||||
|---|---|---|---|---|---|---|
| Second | Third | Annual | Latest | |||
| First | Second | Third | ||||
| Gross domestic product | ||||||
| Advance | 0.10 | 0.09 | 0.04 | −0.13 | 0.11 | −0.01 |
| Second | 0.02 | −0.03 | −0.24 | 0.01 | −0.09 | |
| Third | −0.05 | −0.27 | −0.01 | −0.10 | ||
| First annual | −0.21 | 0.04 | −0.06 | |||
| Second annual | 0.28 | 0.16 | ||||
| Third annual | 0.20 | |||||
| Personal consumption expenditures | ||||||
| Advance | 0.00 | 0.00 | −0.06 | −0.13 | 0.00 | −0.14 |
| Second | 0.00 | −0.04 | −0.14 | 0.00 | −0.13 | |
| Third | −0.05 | −0.14 | 0.00 | −0.14 | ||
| First annual | −0.09 | 0.07 | −0.09 | |||
| Second annual | 0.17 | 0.00 | ||||
| Third annual | 0.15 | |||||
| Gross private domestic investment | ||||||
| Advance | 0.60 | 0.60 | 0.68 | −0.24 | 0.41 | 0.62 |
| Second | 0.01 | 0.09 | −0.83 | −0.16 | 0.04 | |
| Third | 0.08 | −0.84 | −0.17 | 0.02 | ||
| First annual | −0.97 | −0.31 | −0.06 | |||
| Second annual | 0.70 | 0.96 | ||||
| Third annual | 0.76 | |||||
| Fixed investment | ||||||
| Advance | 0.57 | 0.74 | 0.94 | −0.05 | 0.57 | 0.74 |
| Second | 0.18 | 0.38 | −0.61 | 0.03 | 0.18 | |
| Third | 0.20 | −0.78 | −0.16 | 0.00 | ||
| First annual | −1.04 | −0.45 | −0.21 | |||
| Second annual | 0.61 | 0.87 | ||||
| Third annual | 0.75 | |||||
| Exports | ||||||
| Advance | 0.52 | 0.62 | 0.31 | 0.82 | 1.49 | 0.85 |
| Second | 0.10 | −0.21 | 0.26 | 0.90 | 0.33 | |
| Third | −0.32 | 0.14 | 0.78 | 0.22 | ||
| First annual | 0.38 | 1.02 | 0.56 | |||
| Second annual | 0.67 | 0.19 | ||||
| Third annual | 0.19 | |||||
| Imports | ||||||
| Advance | 0.37 | 0.25 | 0.25 | 0.52 | 1.60 | 0.75 |
| Second | −0.10 | −0.12 | 0.14 | 1.18 | 0.38 | |
| Third | 0.00 | 0.25 | 1.31 | 0.50 | ||
| First annual | 0.24 | 1.33 | 0.52 | |||
| Second annual | 1.10 | 0.29 | ||||
| Third annual | 0.23 | |||||
| Federal government | ||||||
| Advance | −0.07 | −0.11 | 0.07 | −0.17 | 0.10 | −0.34 |
| Second | −0.04 | 0.14 | −0.10 | 0.17 | −0.27 | |
| Third | 0.18 | −0.06 | 0.21 | −0.23 | ||
| First annual | −0.23 | 0.04 | −0.43 | |||
| Second annual | 0.30 | −0.20 | ||||
| Third annual | −0.21 | |||||
| State and local government | ||||||
| Advance | 0.05 | 0.01 | −0.23 | −0.13 | 0.54 | 0.07 |
| Second | −0.03 | −0.26 | −0.19 | 0.48 | 0.03 | |
| Third | −0.24 | −0.16 | 0.52 | 0.06 | ||
| First annual | 0.09 | 0.74 | 0.31 | |||
| Second annual | 0.69 | 0.23 | ||||
| Third annual | −0.05 | |||||